nl_spring

SDT-rotor Contents Functions

nl_spring

Purpose

Non linear links/force modeling for time simulation

Syntax

 model=nl_spring('tab',model);
 ...= nl_spring('command', ...)

Description

nl_spring supports non-linear connections and loads for transient analysis. Non linear springs between 2 DOF (see nlspring). loads which depend on DOF values (see DofKuva, DofV), springs between 2 nodes in different bases (see RotCenter), etc. ...). A full list of non-linearities is given in nllist

Standard non-linear simulations are handled by nl_solve. Below is a description of the inner mechanisms of a non-linear simulation with the non-linear toolbox.

After the non linearity definition, a proper TimeOpt is required to set the good fe_time calls to perform a non linear Newmark time integration. A default TimeOpt can be set using nl_spring TimeOpt. It is possible to save transient results on the fly using a properFinalCleanup call, see nl_spring fe_timeCleanupCall , and to reload the same results using fe_simul fe_timeLoad.

The following steps are required for a time simulation

Definition of non-linear properties. These are stored as pro entries of the model stack. The associated property function must handle non-linearities which is currently only the case for p_spring and p_contact.
A non-linearity is always associated with elements or superelements (typically a celas element. A given group of elements can only be associated with a single non-linearity type.
The information needed to describe the non linearity is stored in a .NLdata field.
Model initialization using the an fe_case('assemble') call in fe_time, is followed by the building of a model.NL stack that describes all non-linearities of the model in a format that is suitable for efficient time domain integration. This translation is performed by the nl_spring NL command.
Jacobian computation, see nl_spring NLJacobianUpdate.
Residual computations are performed through mkl_utils. The nominal residual call is r=-fc; mkl_utils('residual', r,model,u,v,a,opt,Case);.

Supported non linearities

See nllist for supported non linearities, and nl_fun to add your own non-linearities.

ConnectionBuild

One can define a set of non linear links between 2 parts of a model using a call of the form
[model,idof]=nl_spring('ConnectionBuild',model,data);
idof is a second optional out argument. It returns the list of DOF concerned by links (it can be useful in order to reduce super elements keeping idof as interfaces DOF for instance). data contains all the information needed to define links. It is a 3 column stack like cell array. First column contains the string 'connection', the second the name of the non linear link described in the third column that contains a data structure with following fields:

.Ci define nodes to connect in first (.C1) and second component (.C2). It can be a vector of NodeId or a screw data structure (slave nodes of the model nodes via RBE3 links, see see sdtweb('fe_case#connectionscrew').
.link defines how to link component 1 to component 2. It is a 1x2 cell array. First cell defines the type of link ('EqualDof' or 'Celas') and the second gives information about the link. For celas link it is a standard element matrix row with 0 replacing NodeId :[0 0 DofId1 DofId2 ProId EltId Kv Mv Cv Bv].
.NLdata (optional) defines non linearity associated to celas link. See the list in list of supported NL. If this field is not present or empty, only linear link is considered.
.PID (optional) is a 1x2 line vector that defines PID (second column of .Node matrix, see sdtweb('node') of connected node (1rst column for 1rst component).
.DID (optional) is the same as above, defining DID (third column of .Node matrix, see sdtweb('node') of connected nodes.

Following example defines a model with a cylinder and a hole in a block. The cylinder is linked to the block by 3 celas preserving the pivot link.

  mo1=demosdt('demoConnection-vol'); % meshes models
  mo1=fe_case(mo1,'fixdof','base','z==-1'); % clamps the cylinder base
  r1=struct('Origin',[0.5 0.5 0.5],'axis',[0 0 1],...
            'radius',.1,'rtol',.01,'length',1,'Npt',-3,...
            'ProId',111,'planes',[]); % Cylinder-side
  r1=nl_spring('ConnectionCyl',r1); % defines planes
  r3=r1; r3.ProId=1; % Block-side
  link={'connection','link1',struct('C1',r3,'C2',r1,...
           'link',{{'celas',[0 0 12345 12345 1000 0 1e9]}})}; % Defines connection
  [model,idof]=nl_spring('ConnectionBuild',mo1,link); % builds connection
  cf=feplot(model); % displays in feplot
  fecom promodelviewon;  fecom('curtab Cases','link1_2');
  def=fe_eig(model,[5 20 1e3]); % computes the first 20 modes
  if length(find(def.data<1e-3))>1; sdtw('_err','connection failed'); end
  cf.def=def; fecom ColorDataAll % displays modes

ConnectionCyl

Utility to fill the .planes field of a cylinder connection in the standard connection screw data structure format (see fe_caseg ConnectionScrew).

dataOut=nl_spring('ConnectionCyl',dataIn);
The dataIn uses fields:

.Origin origin of the cylinder axis, .axis orientation of the cylinder
.rtol radius tolerance for cylinder selection.
.length length of the cylinder.
.Npt number of planes (equally distributed on the whole length). If Npt<0, ends of the cylinder are included in the connection points.
.ProId ProId of the elements containing nodes to connect.

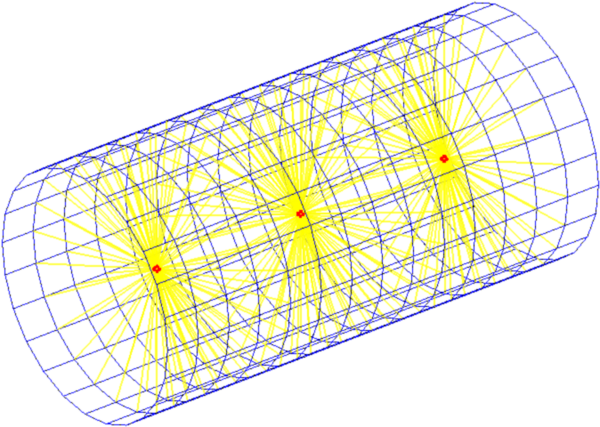
Figure 5.1: ConnectionCyl

InitV

q0=nl_spring('InitV',model,d0,RO);
InitV computes the initial static displacement and velocity associated to a DOF initial position and velocity. d0 is a data structure with field .DOF containing the DofId where initial value is applied and .def containing initial displacement and velocity at this DOF. RO is a optional input argument data structure with following fields that define:

.dt time step for time integration.
.dq increment for initial vel computation.
.Nv] number of time steps to reach d0.def(1) (displacement is imposed as a 0.5(1−cos) time function on these time steps).
.Np number of steps to stabilize at d0.def(1) and d0.def(1)+dq.

If input argument RO omitted, options are get from 'info' 'initvopt' Stack entry. If there is no such entry, InitV parameters are computed using -optim process (see below).

Displacement at q0 and q0+dq is obtained meaning the last Np/10 steps of each stabilization period, and initial velocity is computed from those 2 displacements to match d0.def(2) at d0.DOF.
[q0,RO]=nl_spring('InitV-optim',model,d0); can be used to find input parameters RO. Optimization of dt and Np is performed from given or default values. Parameters dq and Nv are kept at given or default value. First dt is optimized. dt is increased (multiplied by 4) until time integration of the InitV process diverge and last dt that leads to convergence is kept. Then Np is increased by 100 steps until the deformation is converged on the stabilization periods, that is to say that a criteria taking in account standard deviation/mean of the deformation and the ratio of the last Np/10 steps upon previous Np/10 steps on each Np period is less than a tolerance (2.0).
See also t_nlspring('2beam') example.

NL

model=nl_spring('NL',model)
This command is used to build .NL field data for time integration from NLdata field in NL p_spring property entries in the input model Stack. The command option -storefnl can be used to specify the way of computing and storing a non linear effort associated to NL (for those which support it).

NLJacobianUpdate

opt.Jacobian=nl_spring('JacobianCall') returns the callback used to update or initialize the Jacobian ki used in iterative methods. This is the low level implementation of calls documented in nl_solve TgtMdl. The said Jacobian must take non-linearities into account and is thus of the form

(5.3)

the output is controlled by the value of NL.Jacobian.

0 gives no Jacobian.
1 use finite differences to evaluate Jacobian.
2 fixed Jacobian.

For the case of a non-linear spring, the most important gradient of the tabulated law Fu is added as stiffness between the 2 DOF to the stiffness matrix and the most important gradient of Fv to the damping matrix.

For non-linear iterations in a Newmark scheme, the Jacobian is given by

ki=(model.K{3}+kj)+ (opt(2)/opt(1))/dt*(model.K{2}+cj) + 1/opt(1)/dt^2*model.K{1};

Accepted command options, associated to variants of the call are

There are three outputs accessible, being [ki,mo1,C1]=nl_spring('NLJacobian'...).
-noFact not to factorize the output Jacobian. This is useful if further actions are performed on the Jacobian after the standard call.
-TangentMdl to return tangent model. It is assumed that model.K(1:3) correspond to M, C, and K (in this order). u and v variables of caller workspace can be needed.
-TangentMdl-back to return a superelement containing the tangent matrices.
-TangentMdl-back-sepKj to return a superelement containing the tangent matrices split by non linearities.
-ener to compute for each def stored in model.d1 def structure (that is typically computed modes), some associated energies:
- freq frequency in Hz.
- damping damping ratio: .
- enerK total strain energy: .
- enerC .
- NLlink-enerK strain energy for each NL link: .
- NLlink-enerK for each NL link: .

SetPro

model=nl_spring('SetPro ProId i ParamName1 Value1 ...',model)
This command is used to change some nl_spring properties parameters. i is the ProId of corresponding p_spring property, ParamName the name of parameter to change (k for il(3), c for il(5) or the field name in NLdata) and Value the value to assign.

It is possible to define a new property by specifying an NLdata structure in third argument: model=nl_spring('SetPro ProId i',model,NLdata). If the property already exists, the NLdata is interpreted as a string of parameters and parsed to define the fields specified in the given NLdata to the existing one. Command option Edit allows directly merging the existing NLdata to the provided NLdata with priority given to the new fields.

model=nl_spring('Demo1DOF');
% define a non linearity with partial definition of parameters and other by default
NLdata=nl_fun('db data 4') % standard NLdata defintion
% NLdata has fields data, Jacobian (by default) and type
% set in model
model=nl_spring('setpro proid201',model,NLdata);
% edit the nl_fun nl by string keyword
model=nl_spring('setpro proid201 data2',model);

% edit the nl_fun with struct input
% property will be parsed using nl_fun('paramedit')
model=nl_spring('setpro proid201',model,struct('Jacobian',2));
% field Jacobian has been edited, other fields are kept unchanged
model.Stack{end,3}.NLdata

model=nl_spring('setpro proid201',model,struct('NewField','test'));
% you can see that in this case NewField was not set
% as it is not referenced in the nl_fun parameters
model.Stack{end,3}.NLdata

% Force the with struct input with no check
model=nl_spring('setproedit proid201',model,struct('data',10,'NewField','test'));
% in this mode the NewField is propagated regardless of the
% standard nl_fun input
model.Stack{end,3}.NLdata

Standard NLdata structures depend on the non-linear function, see nllist for more details. They can be obtained through the nl_function command db, see nl_fun for more details.

In the case where

GetPro

pro=nl_spring('GetPro',model)
This command is used to get non linear properties in the model stack.

Command option ID allows getting a specific non linear property by specifying its ProId.
Command option type“nl_fun” allows getting the non linear properties of a specific type. See nllist for more details on types of non-linearities.

Follow

The Follow mechanism can be used to observe some variable evolution during the time integration.
opt=fe_simul('Followi',opt);
1st Follow consists in monitoring the number of iteration, the residual norm and displacement increment norm at each time step.

model=nl_spring('Demo1DOF')
opt=stack_get(model,'info','TimeOpt','GetData');
opt=fe_simul('Follow1',opt); % niter norm(r) norm(dq)
def=fe_time(opt,model);

2nd Follow consists in monitoring the def.FNL in iiplot. For the moment the mechanism is different (so note that you can't both tracker niter and FNL), and you only have to specify the field .FnlIiplot equal to 1 in the 'info','OutputOptions' stack entry of the input model, as in following example :

 model=nl_spring('Demo1DOF');
 r1=stack_get(model,'info','OutputOptions','GetData');
 r1.FnlIiplot=1; % define FNL tracker
 model=stack_set(model,'info','OutputOptions',r1);
 opt=stack_get(model,'info','TimeOpt','GetData');
 def=fe_time(opt,model);

TimeOpt

This command returns usual default TimeOpt for non-linear simulations. By default the output is the same as the TimeOptNLNewmark presented below. See also fe_time for TimeOpt definition details.

Supported TimeOpt commands are

TimeOptNLNewmark, or TimeOpt to obtain the TimeOpt for NLNewmark simulations. Use TimeOpt-gamma .51 to introduce numerical damping by directly giving gamma.
TimeOptStat to perform static simulations (see also fe_time nl_solve).
TimeOptTheta to perform time simulations with the θ-method (see fe_time ). Numerical damping can be introduced using TimeOptTheta-alpha .05, the specified α value will be added to θ, so that the coefficient used in the simulations will be θ₁ = θ + α.
TimeOptExplicit to perform time simulations with the explicit Newmark scheme.

The following command options allows setting other TimeOpt fields to their desired value.

dtval time step.
tsN number of time steps.
tendval optional end time
tInitval initial time.
AlphaRval a global Rayleigh damping mass coefficient (applied to the model total mass).
BetaRval a global Rayleigh damping stiffness coefficient (applied to the model total stiffness).
maxNoutN requests an output subsampling strategy such that only N times equally spread over the simulation time span are output.
RelTolval requests a specific relative tolerance for the convergence of iterative schemes.
-gammaval requests a specific γ coefficient (default to .5) of the Newmark scheme. For the non explicit versions, β is adapted to ensure unconditional stability of the scheme.
-thetaval requests a specific θ coefficient (default to .5) of the Theta method.
-acallstr provides a series of command options applied to the AssembleCall generation.
-fcleanstr provides a series of command options applied to the FinalCleanupFcn generation.
-jcallmodel edits the jacobian call to allow late model modification.

Alternatively to providing all these command options in the command string, one can provide a MATLAB struct with equivalent fields as an additional argument.

By adding an SDT model as third argument, the generated TimeOpt will be directly integrated in the model, that will be output.

Sample calls :

% basic call
opt = nl_solve('TimeOpt dt1e-6 ts3e5 maxNout1e4 -acall"lumpedMass"');
% call with struct input
RO=struct('dt',1e-6,'ts',3e5,'maxNout',1e4,...
'acall','lumpedMass');
opt = nl_solve('TimeOptExplicit',RO);
% basic call with model input
model = nl_solve('TimeOpt dt1e-6 ts3e5 maxNout1e4 -acall"lumpedMass"',[],model);
% call with struct and model input
model = nl_solve('TimeOptExplicit',RO,model);

Convergence tests depend on the iteration algorithm and several behaviors can be obtained by modifying RelTol. In any case the absolute value of RelTol is used for the convergence test application; its sign is used to determine the convergence test to be used as described in the following.

For algorithms using iterNewton as IterFcn, as is the case for methods newmark (explicit or not), NLNewmark, and staticNewton.
- using RelTol > 0 tests the convergence of the mechanical residue, relative to value opt.nf. If opt.nf is not provided, the scheme takes in input the norm of the external forces fc at the first time step, or if zero the norm of the first residue of the first time step. If still zero, opt.nf is set to 1. This convergence test is the most widespread as it ensures mechanical stabilization. It is strongly recommended for static computations, or when using large time steps.
- using RelTol < 0 tests the convergence of the displacement correction, relative to the current displacement norm. The idea of this mode is to stop iterating if the correction becomes negligible, this is very useful to limit iterations with little impact on the results in transient simulations with small enough time steps. This must be used with care as this criterion does not imply that the mechanical residue is converged at the end of the time step, it is thus strongly advised to check results convergence.
iterNewton does not support the use of opt.cvg yet.
For algorithms using itertheta_nl as IterFcn, as is the case for method theta,
- using RelTol > 0 tests the convergence of the velocity field, its correction relative to the previous iteration velocity norm.
- using RelTol < 0 tests the convergence of the velocity field, and the model.FNL vector, their correction relative to the previous iteration norm. Stabilization of the model.FNL field may be difficult to attain and very sensitive as this vector can contain heterogeneous data, this mode is then not recommended by default, and use of opt.cvg should be preferred.
iterthetal_nl supports the use of opt.cvg, that forces iteration if set to 1. It is reset to zero at the start of each iteration, but any non-linearity can alter its value by using sp_util('setinput',opt.cvg,ones(1),zeros(1));. Each non-linearity can thus internally test the convergence of its fields of interest and apply a convergence veto if its convergence is not satisfied.

From standard fe_time simulations, the following TimeOpt fields are added or modified

Jacobian field is modified to take into account non linearities, see NLJacobianUpdate.
Residual field is modified to take into account non linearities, and to use mkl_utils to improve computation times, see sdtweb mkl_utils. This should be initialized by nl_spring('ResidualCall').
AssembleCall field is modified, to perform non-linearities initialization after assembly. AssembleCall is the string passed to fe_case, generated by nl_spring('AssembleCall').
OutputInit field is modified to also check non linearities and initialize non-linearities related outputs, this is a callback generated by nl_spring('OutputInitCall').
FinalCleanUpFcn field is modified to perform cleanup on non linearities as well, this is realized through the ExitFcn command option of fe_simulfe_timeCleanUp (see fe_timeTimeOpt), using '-ExitFcn"nl_spring(”fe_timeCleanUp”)"'. This should be initialized by nl_spring('fe_timeCleanupCall).
OutputFcn The output function should be generated by the OutputInit command, since it handles proper interpolation of output as function of the time step, and requires fine tuning in the case of non linear simulations. If nl_spring handles the OutputInit call, OutputFcn is thus reset during initializations. Handling of output time steps using a time vector in OutputFcn is supported.

AssembleCall

The TimeOptAssembleCall must use the -InitFcn callback of fe_caseg Assemble to perform initialization of the non linearities.

Command options are available to tweak the assemble call with minimal user input

MVR To adapt the assemble call for preassembled reduced models. This typically removes the -load command option of the call as this has to be recovered in the MVR itself.
skipMKL No to transform the model matrices into mkls objects.
lumpedMass To adapt the mass matrix mattype to 20 and get a lumped mass matrix.
compose For more complex calls one can redefine from scratch the assemble call line to which the ad hoc initFcn will be added.

ResidualCall

The TimeOptResidual callback should be a call to mkl_utils, that performs optimized matrix vector products, and the computation of non linear forces handled by nl_functions. Command options allows choosing a call adapted to the type of simulations

by default a call adapted to the nlnewmark scheme.
ResidualCallStatic provides a residual adapted to the newton-Raphson schem.
ResidualCallExplicit provides a residual adapted to the newmark explicit scheme.

fe_timeCleanupCall

The TimeOptFinalCleanupFcn callback must use the -ExitFcn of fe_simulto perform post treatments of non linearities. Custom options classical to the fe_simulFinalCleanup call can be added either in the command string or as a string in second argument.

opt.FinalCleanupFcn=nl_spring('fe_timeCleanupCall -cf-1-fullDOF');
% equivalent call with second argument
opt.FinalCleanupFcn=nl_spring('fe_timeCleanupCall','-cf-1-fullDOF');

In addition to the standard fe_simulFinalCleanup, the following command options are available (to be specified outside the ExitFcn callback.

-HDFSave To save the output in a temporary file, and output a v_handle pointer to the saved data. This is useful for RAM optimization matters.
-HDFfnamefname In combination to -HDFSave, to specify the file in which the output will be saved.
-Save To save the output in a temporary file, but keep the results.
-fnamefname In combination to -Save, to specify the file in which the output will be saved.

OutputInitCall

The OutputInit callback is locked for internal nl_spring use. Several command options are available that will be forwarded to the OutputInit procedure

-BlockSaveN To initialize a bufferization of the output of size N. Results will be saved as blocks containing each N saved time steps.
-exit To force exit after initialization. This can be used to check the output format without performing the simulation.
-postFcn To provide a callback that can tweak the output at the end of the OutputInit procedure. This can be used for example to initialize out.Post post treatments.

TimeOutputOptions

Fine tuning of fe_time output can be achieved by specifying an 'info','OutputOptions' case entry.

Accepted fields for the OutputOptions structure are

.FnlAllT if defined and equal to 1, non-linear loads are saved at all time steps.
.FnlIiplot if defined and equal to 1, non linear loads are displayed in an iiplot figure as curve FNL. If the display timer associated with this figure does not stop automatically, you can stop it with cingui('TimerStop').

mkl_utils

Non linearities are treated by mkl_utils mex file. Details are provided in mkl_utils.

rheo2NL

OBSOLETE. Use now nl_spring NL.
NL=nl_spring('rheo2NL',model,DOF,offset);
This command is used to convert rheological data into a structure of data understandable for NLforce command. DOF is the list of the DOF coherent with u and v arguments of NLforce command. Offset is optional. It is a structure of data with fields .DOF and .def that defined 0 reference for Fu and Fv tab laws.

tab

model=nl_spring('tab',model);
This command is used to convert formal rheological description data stored in model.Stack to a tabulated law description. The format is likely to change due to optimization of the compiled functionality in mkl_utils (see mkl_utils).

BlockSave,BlockLoad

Undocumented intermediate save of a time block for long simulations that do not fit in memory.