
 PDF Index
PDF IndexSDT-rotor
Contents
Functions

 PDF Index
PDF Index |
Purpose
nl_maxwell describes rheological models using stiffness and damping. Deprecated implementation that should now be called with an nl_inout.
| .type | 'nl_maxwell' |
| .lab | Label of the non linearity. |
| .Sens | Observation definition. Cell array of the form {SensType,SensData} where SensType is a string defining the sensor type and SensData a matrix with the sensor data (see sdtweb sensor). |
| .Load | data structure defining the command as a load (with .DOF and .def fields). |
| .SE | superelement that defines the rheological model. Only matrices are used (.K field). Mass matrix is ignored. The .DOF field is unused and first DOF are assumed to be the observations defined, and following correspond to internal states. |
| .NLsteps | Number of sub steps for the integration. |
| .StoreFNL | strategy to store FNL output, should be initialized from StoreType. |
| Ncell | number of cells. |
Jacobian is computed using a Guyan condensation keeping only the observation (internal states are condensed) to obtain tangent damping and stiffness.
Internal states are integrated using an independent finite differences explicit scheme, with the same step of time as the main scheme, or a subsampling NL.NLsteps times.
At the first residue computation, the initial internal states are computed according to initial condition in terms of displacements and velocities through a time integration until variation of speed between the 2 last computed steps is lower than opt.RelTol.
Force on the observation DOF (F), displacement (Qc) and velocity (dQc) of the internal DOF, displacement and velocity observations are stored in the NL output.
The command nl_spring db Fu"type" is a database of generalized Maxwell rheological models. type can be:
The example of the standard viscoelastic model is detailed here as an illustration. The standard viscoelastic model, also known as Zener model, is composed by a spring (K0) in parallel with another spring (K1) and a serial dashpot (C1) as displayed figure 5.2.
In the Laplace domain, the relation between the relative load and the relative displacement is given by
| (5.4) |
where p and z are respectively the pole and the zero of the model
| (5.5) |
| (5.6) |
The maximum loss factor is
| (5.7) |
and obtained for pulsation
| (5.8) |
K0 is the static stiffness of the model. Typically K1=K0/2 and C1 is defined so that the damping is maximal for the frequency of interest.
Following example considers K0=1000N/m, K1=500N/m and C1=1.4Ns/m. These parameters lead to a maximum loss factor of 20.14% for a frequency of 46.41Hz. The module and the loss factor are represented in figure 5.3.
Following example consists in a mass of 1e-2kg linked to the ground by the Zener model. Initial displacement corresponding to a 1N load on the mass is imposed and then a time simulation is performed.
% parameters param.m=1e-2; param.dt=1e-4; param.N=1e3; param.k0=1e3; param.k1=param.k0/2; param.c1=1.4; % zener parameters % define model model=struct('Node',[1 0 0 0 0 0 0],... 'Elt',[Inf abs('mass1') 0; 1 0 0 param.m 0 0 0]); % define nl_maxwell data data=nl_maxwell(sprintf('db Fu"zener k0 %.15g k1 %.15g c1 %.15g"',.... param.k0,param.k1,param.c1)); data.Sens{2}=1.03; % translation sensor defining nl_maxwell inputs % define associated property r1=p_spring('default'); r1=feutil('rmfield',r1,'name'); r1.NLdata=data; r1.il(3)=param.k0; r1.il(1)=100; model=stack_set(model,'pro','zener',r1); % define option for time integration opt=d_fetime('TimeOpt'); opt.NeedUVA=[1 1 1]; opt.Follow=1; opt.RelTol=-1e-5; opt.Opt(7)=-1; % factor type sparse opt.Opt(4)=param.dt; opt.Opt(5)=param.N; % NSteps %opt.IterEnd='eval(opt.Residual)'; % to compute real FNL for current state % Initial state r1=data.SE.K{3}\[1;0]; r1=r1(1); % initial displacement for 1N load model=stack_set(model,'curve','q0',struct('def',r1,'DOF',1.03)); % Time computation def0=fe_time(opt,model); ci=iiplot; % compute % The same but NL as a model SE2=data.SE; SE2.Elt(end+1:end+2,1:6)=[Inf abs('mass1'); 1 0 0 param.m 0 0]; SE2=fe_caseg('assemble -secdof -matdes 2 3 1 -reset',SE2); r1=SE2.K{3}\[1;0]; %r1=r1(1); SE2=stack_set(SE2,'curve','q0',struct('def',r1,'DOF',SE2.DOF)); def20=fe_time(opt,SE2); % compute F20=SE2.K{2}*def20.v+SE2.K{3}*def20.def; F20=F20(1,:); % zener labs: {'zener-F1','zener-q1','zener-q1-1','zener-dq1','zener-dq1-1'} NL20=struct('X',{{def20.data {'LIN-F1';'LIN-Qc1';'LIN-dQc1';'LIN-unl1';'LIN-vnl1';'ft'}}},... 'Xlab',{fe_curve('datatypecell','time')},... 'Y',[F20' (fe_c(def20.DOF,1.03)*def20.def)'... (fe_c(def20.DOF,3.03)*def20.def)'... (fe_c(def20.DOF,1.03)*def20.v)'... (fe_c(def20.DOF,3.03)*def20.v)' zeros(size(def20.def,2),1) ]); NL20.name='NLfromLIN'; iicom('curveinit',{'curve','NL(1)',ci.Stack{'NL(1)'}; 'curve',NL20.name,NL20}); A=ci.Stack{'NL(1)'}.Y(2:end,:);B=NL20.Y(2:end,:);t=NL20.X{1}(2:end);i2=any(A); if norm(A(:,i2)-B(:,i2),'inf')/norm(B,'inf')>0.01 figure(1);plot(t,A,'--o',t,B,'-') sdtw('_err','something has changed') end
DofKuva defines a non linear load of the form
a vDofe [K]{V} with a scalar coefficient a, a scalar vDof extracted from displacement, velocity or acceleration, and V a field specified as follows
| .type | 'DofKuva' |
| .lab | Label of the non linearity. |
| .Dof | Dof of Case.DOF. |
| .Dofuva | [1 0 0] for displacement Dof, [0 1 0] for velocity and [0 0 1] for acceleration. |
| .MatTyp | Type of the matrix K (see MatType). Desired matrix is automatically assembled before time computation. |
| .factor | Scalar factor a. |
| .exponent | Exponent of the DOF. |
| .uva | Type of vector V: [1 0 0] for displacement, [0 1 0] for velocity and [0 0 1] for acceleration. |
For example one can take in account gyroscopic effect in a time computation with a NL of the form
model=stack_set(model,'pro','DofKuva1005', ... % gyroscopic effects struct('il',[1005 fe_mat('p_spring','SI',1) 0 0 0 0 0],... 'type','p_spring','NLdata',struct(... 'type','DofKuva','lab','gyroscopic effect', ... 'Dof',1.06,'Dofuva',[0 1 0],'MatTyp',7,... 'factor',-1,'exponent',1,'uva',[0 1 0])));
DofV defines a non linear effort of the following form (product of a fixed vector and a dof)
(u)exponent.V NDdata fields for this non-linearity are
| .type | 'DofV' |
| .lab | Label of the non linearity. |
| .Dof | Dof of Case.DOF. |
| .Dofuva | [1 0 0] for displacement Dof, [0 1 0] for velocity and [0 0 1] for acceleration. |
| .exponent | Exponent of the DOF. |
| .def | data structure with fields .def which defines vector V and .DOF which defines corresponding DOF. |
nl_spring defines a non linear load from rheological information (stop, tabulated damping or stiffness laws etc.) between 2 DOF.
To define a non linear spring, one has to add a classic celas element, linear spring between only 2 DOF. The non linear aspect is described by associated properties as a 'pro' entry in the model Stack.
One can describe non linearity by a formal rheological description using one or more of following fields in the pro Stack entry:
This information will be converted in tabulated laws Fu and Fv using nl_spring tab (low level call that should be automatically called at the beginning of time computation).
One can also describe non linearity with a tabulated effort / relative displacement and effort / relative velocity law between the DOF (dof2-dof1), respectively in the Fu and Fv fields of the pro Stack entry. First column of Fu (resp. Fv) gives the relative displacements (resp. velocities) and second column gives the efforts. One can give a coefficient av factor of Fv depending on relative displacement as a third column of Fu. It can be useful to describe a non linearity depending on relative displacement and relative velocity. Force applied is F=av(du).Fv(dv). It is used in particular to describe damping in a stop (.But NL).
Following example performs a non linear time computation on a simple 2-node model:
RT=struct('nmap', vhandle.nmap); % sdtweb d_fetime Mesh2DOF % For meshing scrip % sdtweb d_fetime LegacyBumpStop % For NLdata definition li={'MeshCfg{"d_fetime(2DOF):LegacyBumpStop{Z0}"}' 'SimuCfg{Imp{1m,10,uva110}}'; % implicit NLNewmark simulation 'RunCfg{Time}'};disp(comstr(li(1:2:end)',-30)) RT.nmap('CurExp')=li; sdtm.range(RT); model=RT.nmap('CurModel');def=model.nmap('CurTime'); li{3}='SimuCfg{Exp{1m,10,uva110}}'; RT.nmap('CurExp')=li;% Same using explicit sdtm.range(RT);mo2=RT.nmap('CurModel');d2=model.nmap('CurTime'); figure(10);clf;% plot some comparison between results subplot(211);plot(def.data,[def.def' d2.def']);xlabel('Time [s]');ylabel('displacement') subplot(212);plot(def.data,[def.v' d2.v']);xlabel('Time [s]');ylabel('velocity') legend('Implicit','Explicit');setlines; sdth.os(10,'@OsDic',{'ImGrid','ImSw80','ImTight'})
Following example deals with a clamped-free beam, with a bilateral bump stop at the free end.
% define model: L=1; b=1e-2; h=2e-2; e=1e-3; % dimensions model=[]; model.Node=[1 0 0 0 0 0 0; 2 0 0 0 L 0 0]; model.Elt=[Inf abs('celas') 0 0; 2 0 2 0 100 1 110 0; % linear celas Inf abs('beam1') 0 0; 1 2 1 1 0 1 0 0 ]; model=feutil(sprintf('RefineBeam %.15g',L/20),model); model=fe_case(model,'FixDof','base',1); % clamps 1st end model=fe_case(model,'FixDof','2D',[0.03;0.04;0.05]); % 2D motion % model properties: model.pl=m_elastic('dbval 1 steel'); model.il=p_beam(sprintf('dbval 1 BOX %.15g %.15g %.15g %.15g',b,h,e,e)); % Bump stop NL: model=stack_set(model,'pro','celas1',... struct('il',[100 fe_mat('p_spring','SI',1) 1e-9 0 0 0 0],... 'type','p_spring',... 'NLdata',struct('type','nl_inout',... 'but',[0.02 5e2 0 -0.02 5e2 0],... % gap knl cnl... 'umin',3))); if 1==1 model=fe_case(model,'DofLoad','in',struct('DOF',2.02,'def',50)); model=fe_curve(model,'set','input','TestStep t1=0.02'); else f=linspace(12,18,3); model=fe_case(model,'DofLoad','in',struct('DOF',2.02,'def',1)); model=fe_curve(model,'set','input',sprintf('Testeval cos(%.15g*t)',f(1)*2*pi)); end model=fe_case(model,'setcurve','in','input'); % Time computation: opt=d_fetime('TimeOpt dt=1e-3 tend=10'); opt.NeedUVA=[1 1 0]; def=fe_time(opt,model);
The Rotcenter joint is used to introduce a penalized translation link between two nodes A and B (rotation DOFs of NL entry are ignored), where the motion of A is defined in a rotating frame associated with angle θA and large angle rotation RLG(θA). The indices G and L are used to indicate vectors in global and local coordinates respectively.
The positions of nodes are given by
| (5.9) |
which leads to expressions of the loads as
| (5.10) |
To account for viscous damping loads in the joints, one must also compute velocities. Using (2.2), one obtains
| (5.11) |
Velocity computations are currently incorrect with uA ignored in the rotation effect. So that viscous damping loads can be added
| (5.12) |
For a linearization around a given state (needed for frequency domain computations or building a sensor observation matrix),
| (5.13) |
In global basis, stiffness matrix of a celas link is given by
| (5.14) |
which leads to the following stiffness matrix
| (5.15) |
where qA DOFs are in the local basis (motion relative to the shaft in its initial position) and qB are in the global frame.
data describing this link is stored in model stack as a p_spring pro entry. Stiffness and damping are stored respectively as 3rd and 5th column of the data.il field (standard linear spring, see sdtweb('p_spring')).
NDdata fields:
This non linearity can be used to connect 2 points A and B, where the motion of A is defined in a rotating frame associated with angle θA and large angle rotation RLG(θA). More generally A and B are no real nodes but defined implicitly as observation matrices. nl_rotcenter is an extension of RotCenter documented above, using observation matrices which is more general.
An example can be found in t_nlspring 2beam.
Default uses the damping and stiffness defined in the il field of the p_spring pro entry to model a linear spring/damper between the 2 parts (stiffness il(3) and damping il(5)).
Defining a xb parameter, the Excite NONL law will be applied instead of the spring/damper. Parameter that are to be defined are
Stiffness and damping at initial position are given in corresponding p_spring properties il(3) and il(5).
For example:
cf.mdl=nl_spring('setpro ProId 103 k 371 c 2000e-3 xb 0.03 kb 37100 cb 5',cf.mdl);
The rod1 non-linear connection is a simple penalized rigid link. One considers two nodes A and B (see figure 5.4).
Currently, one can introduce masses at points A and B. mass2 elements should be used to account for the actual position of the center of gravity.
The global non linear load associated with the rod is thus
| (5.16) |
which accounts for a load proportional to the length fluctuation around L0 (penalized rod model).
When linearizing, one considers a strain energy given by kr || qB−qA′ ||2 with the motion at node A′ being related to the 6 DOFs at node A by
| (5.17) |
Node A node is free to rotate. The linearized stiffness thus corresponds to an axial stiffness in the direction of the rod. The computation of the stiffness is however based on the current position of the extremity nodes, a difficulty in model manipulations is thus to translate these nodes.
data describing this link is stored in model stack as a p_spring pro entry. Stiffness and damping are stored respectively as 3rd and 5th column of the data.il field (standard linear spring, see sdtweb('p_spring')). NL information is stored in the data.NLdata field which has itself following fields :
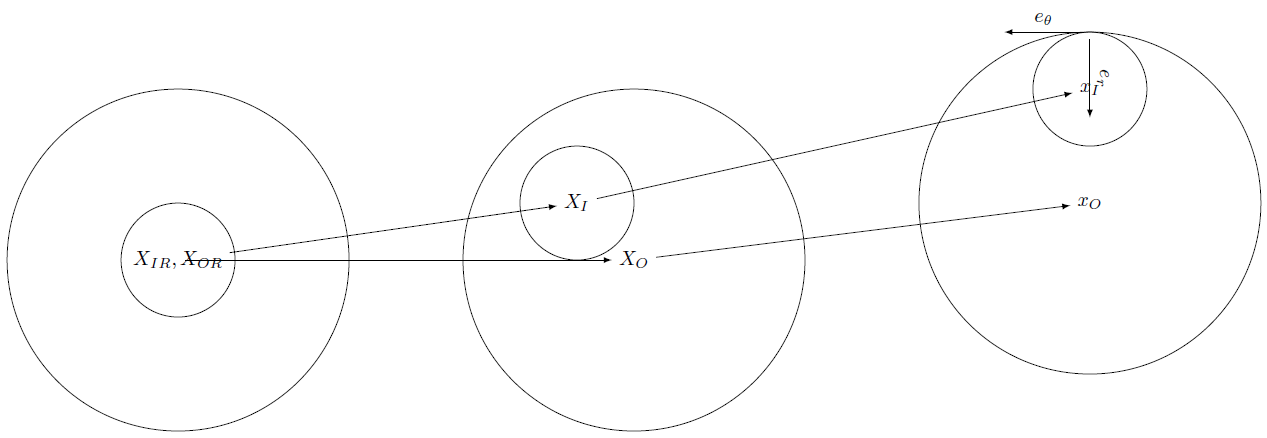
This non-linearity implements non-linear contact between two cylinders of radius RO for the outer cylinder and RI for the inner cylinder with motion defined on the cylinder center line. Assuming the mesh to be defined in an updated Lagrangian configuration where the center lines XI and XO at not coincident, the positions in a deformed states are given by xI=XI+uI and xO=XO+uO.
Contact may only occur when the cylinders are not centered. When the two cylinders are not centered the non-linear observation is given by
| (5.18) |
From this distance between the center lines, a cylindrical basis is defined with er(q) along the direction from xI to xO and eθ forming a direct basis with the cylinder axis (kept constant from the initial value of the updated lagrangian position).
The functional definition of the contact force uses the gap in the er direction defined by
| (5.19) |
where RO−RI=d is stored as parameter NLdata.d and the contact leads to two opposite forces on the cylinder center lines
| (5.20) |
The current implementation assumes rotations to be small enough to ignore the difference between er and the corresponding vector Er in the upated Lagrangian configuration.
If update of mesh leads to lateral slip, then uI may account for longitudinal position of the contact point along the beam using shapes functions.
When linearizing the contact around a given point, the stiffness ∂ f∂ g only occurs in the er direction.


