Simple 2DOF model of shaft with disk

SDT-rotor Contents Functions

4.2 Simple 2DOF model of shaft with disk

This section is about the simple 2 DOF rotor model described in chapter 2 of Lalanne and Ferraris [7].

Figure 4.3: Simple model of rotor.

The disk is rigid, the shaft is described by 2 sin shape functions f(y)=sin(π y/L) where L is the length of the shaft.
Bearing at y=L/3 is represented by 2 additional stiffness and damping. K_bearing=sin(2π/3) [

kxx	kxz
kzx	kzz

] C_bearing=sin(2π/3) [

cxx	cxz
czx	czz

]

The 2 DOF are considered in the global fixed frame.

(4.11)

For an unbalanced mass mb at a position of L/3 on the shaft and at a distance of db of the rotation axis F=m^*dbΩ²{

sin(Ω t)

cos(Ω t)

} where m^*=sin(π/3)mb.
For a simple asynchronous load of amplitude f0 rotating at sΩ F=f0 {

sin(sΩ t)

cos(sΩ t)

Frequency analysis is performed.
Harmonic solutions are computed under the form ℜ(Q₀ exp(i s Ω t)) (s=1 for unbalanced mass and s<>1 for asynchronous load).

Implementation of this case can be found in d_rotor Lalanne2DOF. One can define values of parameters (kxx, czx, m, a, mb, f0, s etc. ...) as fields of a data structure r1 given as argument : d_rotor('Lalanne2DOF',r1). A campbell and frequency forced response are then computed at the rotation speeds defined (in RPM) in the field .om of the parameter data structure. One can ask only for the model using model=d_rotor('Lalanne2DOFMdl',r1);.
If this first case, no bearing is considered (K_bearing=0 and C_bearing=0).

beta=0;
r1=struct('om',linspace(0,9e3,101),'s',1,...
     'kxx',0,'kzz',0,'kxz',0,'kzx',0,...
     'cxx',1e2*beta,'czz',5e2*beta,'cxz',0,'czx',0);
R1=d_rotor('TestLalanne2DOF',r1)

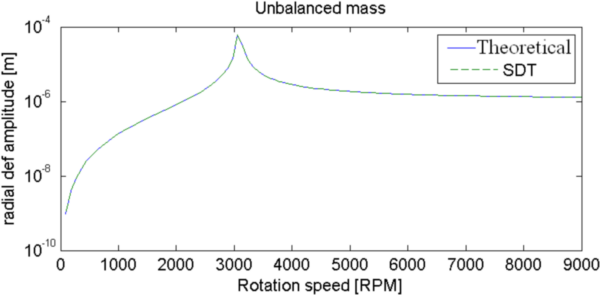
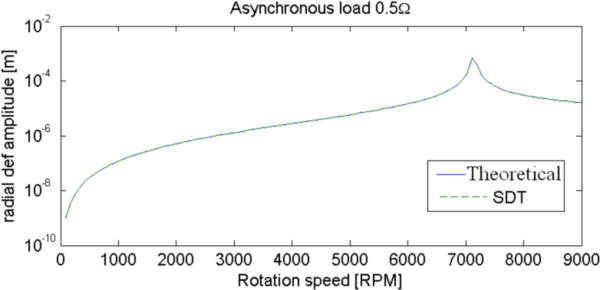
Figure 4.4: Campbell diagram. Symmetric rotor without bearing.

Figure 4.5: Response to an unbalanced load (left) and asynchronous load (right). Symmetric rotor without bearing.

Maximum response for unbalanced mass is obtained for the exact critical rotation speed of forward mode computed in the Campbell (3089 RPM). This speed is the same as in Lalanne theoretical expression.

Bearing stiffness along z is now taken in account so that rotor is not symmetric. kzz=5e5 and kxx=kxz=kzx=0. There is no damping in the bearing: C_bearing=0).

beta=0;
r1=struct('om',linspace(0,9e3,101),'s',1,...
     'kxx',0,'kzz',5e5,'kxz',0,'kzx',0,...
     'cxx',1e2*beta,'czz',5e2*beta,'cxz',0,'czx',0);
R1=d_rotor('TestLalanne2DOF',r1)

Figure 4.6: Campbell diagram. Asymmetric rotor with z stiffness bearing.

Now the 2 modes are not at the same frequency for Ω=0.

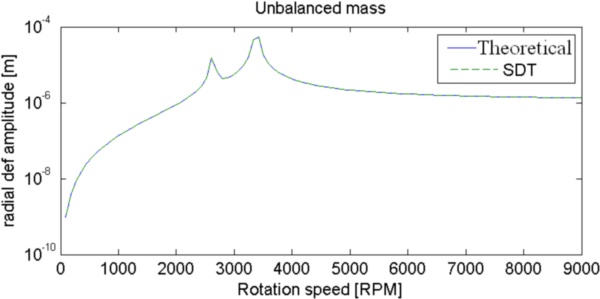
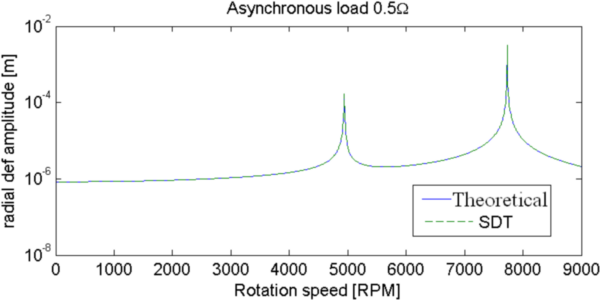
Figure 4.7: Response to an unbalanced load (left) and asynchronous load (right). Asymmetric rotor with z bearing stiffness.

Now there are 2 maximums of response that match critical rotation speeds for both forward and backward modes. This is the same for the asynchronous load.
Bearing stiffness along z is taken in account so that rotor is not symmetric. kzz=5e5, kxx=1e5 and kxz=kzx=0. Damping in the bearing is also considered with cxx=100β, czz=500β and cxz=czx=0.

beta=15;
r1=struct('om',linspace(0,20e3,201),'s',1,...
     'kxx',1e5,'kzz',5e5,'kxz',0,'kzx',0,...
     'cxx',1e2*beta,'czz',5e2*beta,'cxz',0,'czx',0);
d_rotor('TestLalanne2DOF',r1)

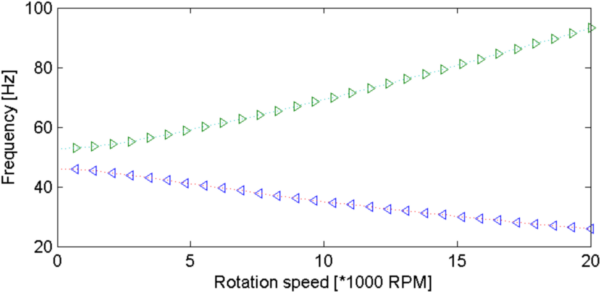
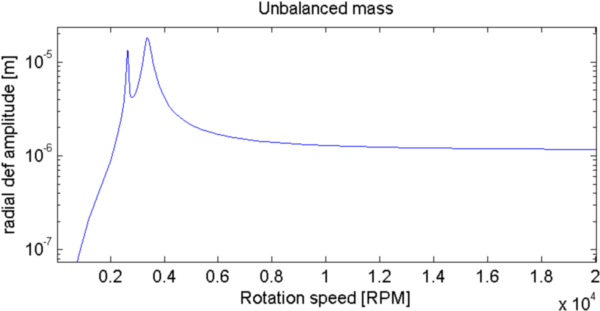
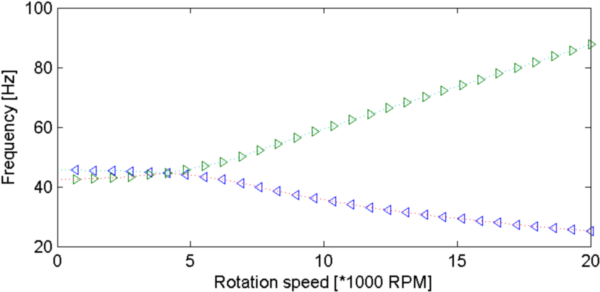
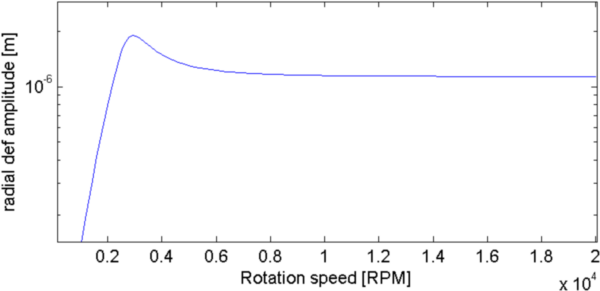
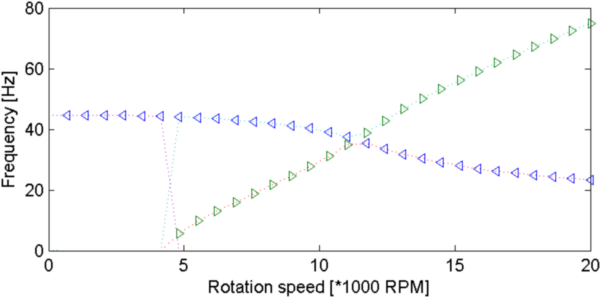
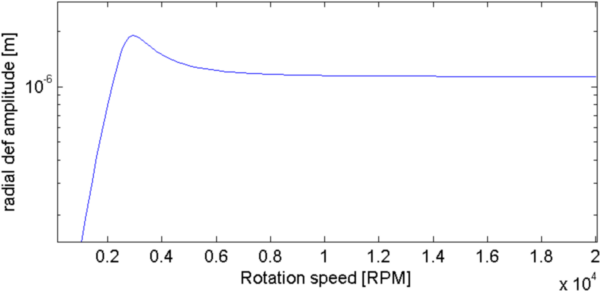
Figure 4.8: Campbell (left) and Responses to unbalanced load (right) for different damping (top:β=1, middle:β=15 and bottom:β=26). Asymmetric rotor with z bearing stiffness and damping.

Backward and forward mode can cross each other in the Campbell diagram. Asymmetry leads to the excitation of the backward mode. Damping leads to a more spread resonance response.