id_nor

id_nor#

Purpose

Identification of normal mode model, with optimization of the complex mode output shape matrix.

NOR               = id_nor(ci.Stack{'IdMain'})
NOR               = id_nor( ... )
[om,ga,phib,cphi] = id_nor( ... )
[new_res,new_po]  = id_nor( ... )
[ ... ]           = id_nor(IdResult,ind,opt,res_now)

Description

id_nor is meant to provide an optimal transformation (see details in [19] or section 2.9.3) between the residue (result of id_rc) and non-proportionally damped normal mode forms

(10.27)

The output arguments are either

the standard normal mode model freq,ga,phib,cphi (see nor) when returning 4 outputs.
the associated normal model data structure NOR when returning one output.
or the residues of the associated model new_res and poles po (see res ) when returning 2 outputs. With this output format, the residual terms of the initial model are retained.

The algorithm combines id_rm (which extracts complex mode output shape matrices cψ from the residues res and scales them assuming the system reciprocal) and psi2nor (which provides an optimal second order approximation to the set of poles po and output shape matrices cψ).

Since the results of psi2nor can quite sensitive to small errors in the scaling of the complex mode outputs cψ, an optimization of all or part (using the optional argument ind to indicate the residues of which poles are to be updated) collocated residues can be performed. The relative norm between the identified residues res and those of the normal mode model is used as a criterion for this optimization.

Three optimization algorithms can be selected using opt (1: id_min of the Structural Dynamics Toolbox, 2: fmins of MATLAB, 3: fminu of the Optimization Toolbox). You can also restart the optimization using the residues old_res while still comparing the result with the nominal res using the call

 [new_res,po] = id_nor(res,po,idopt,ind,opt,old_res)

Notes

id_nor is only defined if IDopt.Reciprocity is 1 FRF or MIMO (12) and for cases with more sensors than modes (check IDopt.NSNA). id_nor may not work for identifications that are not accurate enough to allow a proper determination of normal mode properties.

In cases where id_nor is not applicable, normal mode residues can be identified directly using id_rc with IDoptFit='Normal' or an approximate transformation based on the assumption of proportional damping can be obtained with res2nor.

id_nor does not handle cases with more poles than sensors. In such cases res2nor can be used for simple approximations, or id_nor can be used for groups of modes that are close in frequency.

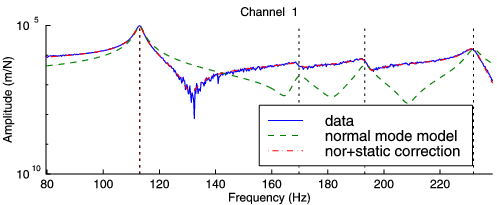
Residual terms can be essential in rebuilding FRFs (see figure above taken from demo_id) but are not included in the normal mode model (freq, ga, phib, cphi). To include these terms you can use either the residues new_res found by id_nor

 xf = res2xf(new_res,po,w,idopt)

or combine calls to nor2xf and res2xf

 xf = nor2xf(om,ga,phib,cphi,w) + ...
      res2xf(res,po,w,idopt,size(po,1)+1:size(res,1))

Example

 ci=demosdt('demo gartidest')
 % The collocated transfer is measured in opposite direction to the input one
 if ci.Stack{'Test'}.dof(4,2)~=1012.03;
  ci.Stack{'Test'}.xf=-ci.Stack{'Test'}.xf; % Needed to have positive driving point FRFs
  ci.IDopt.Reciprocity='1 FRF'; % Reciprocity to scale modes using collocated transfer
  ci.Stack{'Test'}.dof(:,2)=1012.03; idcom('est');
 end
 nor = id_nor(ci.Stack{'IdMain'});
 ci.Stack{'curve','IIxh'}=nor2xf(nor,ci.Stack{'Test'}.w,'hz struct acc');
 iicom('iixhon')