7.15  Internal data structure reference

7.15.1  Element functions and C functionality

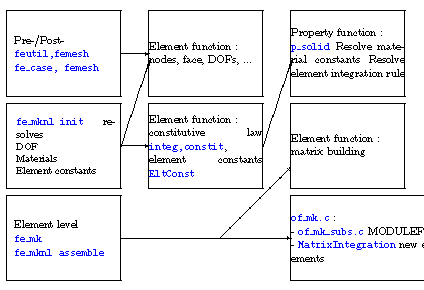
In OpenFEM, elements are defined by element functions. Element functions provide different pieces of information like geometry, degrees of freedom, model matrices, …

OpenFEM functions like the pre-processor femesh, the model assembler fe_mk or the post-processor feplot call element functions for data about elements.

For example, in the assembly step, fe_mk analyzes all the groups of elements. For each group, fe_mk gets its element type (bar1, hexa8, …) and then calls the associated element function.
First of all, fe_mk calls the element function to know what is the right call form to compute the elementary matrices (eCall=elem0('matcall') or eCall=elem0('call'), see section 7.16.6 for details). eCall is a string. Generally, eCall is a call to the element function. Then for each element, fe_mk executes eCall in order to compute the elementary matrices.

This automated work asks for a likeness of the element functions, in particular for the calls and the outputs of these functions. Next section gives information about element function writing.

7.15.2  Standard names in assembly routines

cEGI	vector of element property row indices of the current element group (without the group header)
constit	real (double) valued constitutive information. The constit for each group is stored in Case.GroupInfo{jGroup,4};.
def.def	vector of deformation at DOFs. This is used for non-linear, stress or energy computation calls that need displacement information.
EGID	Element Group Identifier of the current element group (different from jGroup if an EGID is declared).
elt	model description matrix. The element property row of the current element is given by elt(cEGI(jElt),:) which should appear in the calling format eCall of your element function.
ElemF	name of element function or name of superelement
ElemP	parent name (used by femesh in particular to allow property inheritance)
gstate	real (double) valued element state information.
integ	int32 valued constitutive information.
jElt	number of the current element in cEGI
jGroup	number of the current element group (order in the element matrix). [EGroup,nGroup]=getegroup(elt); finds the number of groups and group start indices.
nodeE

NNode

node identification reindexing vector. NNode(ID) gives the row index (in the node matrix) of the nodes with identification numbers ID. You may use this to extract nodes in the node matrix using something like node(NNode(elt(cEGI(jElt),[1 2])),:) which will extract the two nodes with numbers given in columns 1 and 2 of the current element row (an error occurs if one of those nodes is not in node). This can be built using NNode=sparse(node(:,1),1,1:size(node,1).

pointers

one column per element in the current group gives.

7.15.3  Case.GroupInfo cell array

The meaning of the columns of GroupInfo is as follows

DofPos Pointers Integ Constit gstate ElMap InfoAtNode EltConst

DofPos	int32 matrix whose columns give the DOF positions in the full matrix of the associated elements. Numbering is C style (starting at 0) and -1 is used to indicate a fixed DOF.
pointers

integ	int32 matrix storing integer values used to describe the element formulation of the group. Meaning depends on the problem formulation and should be documented in the property function (p_solid BuildConstit for example). The nominal content of an integ column (as return by the element integinfo call) is MatId,ProId,NDofPerElt,NNodePerElt,IntegRuleType where integrules(ElemP,IntegRuleType) is supposed to return the appropriate integration rule.
constit	double matrix storing integer values used to describe the element formulation of the group. Meaning depends on element family and should be documented in the element property function (p_solid BuildConstit for example).
gstate	a curve with field .Y describing the internal state of each element in the group. Typical dimensions stress, integration points, elements so that .Y has size Nstrain× Nw × NElt. The labels in .X{1} can be used to find positions in the .Y matrix. The .X{2} should contain the gauss point locations within the reference element. Automated generation of initial states is discussed in section 7.13.
	Users are of course free to add any appropriate value for their own elements, a typical application is the storage of internal variables. For an example of gstate initialization see fe_stress thermal.
	the old format with a double matrix with one column per element is still supported but will be phased out.
ElMap	int32 element map matrix used to distinguish between internal and external element DOF numbering (for example : hexa8 uses all x DOF, then all y ... as internal numbering while the external numbering is done using all DOFs at node 1, then node 2, ...). The element matrix in external sort is given by k_ext=ke(ElMap). EltConst.VectMap gives similar reordering information for vectors (loads, ...).
InfoAtNode	a structure with .NodePos (int32) with as many columns as elements in the group giving column positions in a .data field. Each row in .data corresponds to a field that should be described by a cell array of string in .lab used to identify fields in assembly, see nodeE. Initialization for a given element type is done the GroupInit phase, which uses pro.MAP fields (see section 7.13). Typical labels for orientation are {'v1x','v1y','v1z','v2x','v2y','v2z'}
	Obsolete format : double matrix whose rows describe information at element nodes (as many columns as nodes in the model).
EltConst	struct used to store element formulation information (integration rule, constitutive matrix topology, etc.) Details on this data structure are given in section 7.15.4.

7.15.4  Element constants data structure

The EltConst data structure is used in most newer generation elements implemented in of_mk.c. It contains geometric and integration rule properties. The shape information is generated by calls to integrules. The formulation information is generated p_function const calls (see p_solid, p_heat, ...).

.N	nw × Nnode shape functions at integration points
.Nr	nw × Nnode derivative of shape function with respect to the first reference coordinate r
.Ns	nw × Nnode derivative of shape function with respect to the second reference coordinate s
.Nt	nw × Nnode derivative of shape function with respect to the second reference coordinate t
.w	Nnode × 4 gives the r,s,t positions (with t=0 for 2D) of Gauss points within the element and the integration rule weight in column 4.
.NDN	Nshape × nw (1+Ndim) memory allocation to store the shape functions and their derivatives with respect to physical coordinates [N N,x N,y N,z]. of_mk currently supports the following geometry rules 3 3D volume, 2 2D volume, 23 3D surface, 13 3D line (see integrules BuildNDN for calling formats). Cylindrical and spherical coordinates are not currently supported. In the case of rule 31 (hyperelastic elements), the storage scheme is modified to be (1+Ndim) × Nshape × nw which preserves data locality better.
.jdet	Nw memory allocation to store the determinant of the Jacobian matrix at integration points.
.bas	9× Nw memory allocation to store local material basis. This is in particular used for 3D surface rules where components 6:9 of each column give the normal.
.Nw	number of integration points for output (inferior to size(EltConst.N,1) when different rules are used inside a single element)
.Nnode	number of nodes (equal to size(EltConst.N,2)=size(EltConst.NDN,1))
.xi	Nnode × 3 reference vertex coordinates
.VectMap	index vector giving DOF positions in external sort. This is needed for RHS computations.
.CTable	low level interpolation of constitutive relation based on field values. Storage as a double vector is given by [Ntables CurrentValues (Ntables x 7) tables] with CurrentValues giving [i1 xi si xstartpos Nx nodeEfield constit(pos_Matlab)]. Implementation is provided for m_elastic to account for temperature dependence, fe_mat to generate interpolated properties.