
 PDF Index
PDF Index
Contents
Functions

 PDF Index
PDF Index |
This example deals with a multi-layer composite plate with 4 piezoceramic patches. The geometry is represented in Figure 2.1. It corresponds to a cantilevered composite plate with 4 piezoelectric patches modeled using the p_piezo Shell formulation.

Figure 2.1: Geometric details of the composite plate with 4 piezoceramic patches
The material properties of the composite plate and the piezoceramic patches are given in Table 2.1. The composite material is made of 6 identical layers (total thickness of 1.3 mm), and the piezoelectric material corresponds to the Sample_ULB material in m_piezo Database.
Property Value Composite layers Ex 41.5 GPa Ey 41.5 GPa Gxy 3.35 GPa νxy 0.042 ρ 1490 kg/m3 Piezoceramic patches E 65 GPa ν 0.3 ρ 7800 kg/m3 thickness 0.25 mm d31 -205 10−12 pC/N (or m/V) d32 -205 10−12 pC/N (or m/V) є33T 2600 є0 є0 8.854 10−12 Fm−1
Table 2.1: Material properties of the plate and the piezoceramic patches
The first step consists in the creation of the model, the definition of the boundary conditions, and the definition of the default damping coefficient.
( d_piezo('TutoPlate_4pzt_single-s1')
)
The resulting mesh is shown in Figure 2.2
d_piezo('TutoPlate_4pzt_single-s1')
)
The resulting mesh is shown in Figure 2.2
% See full example as MATLAB code in d_piezo('ScriptPz_plate_4pzt_single') %% Step 1 - Build model and visualize model=d_piezo('MeshULBplate'); % creates the model model=fe_case(model,'FixDof','Cantilever','x==0'); % Set modal default zeta based on loss factor of material 1 model=stack_set(model,'info','DefaultZeta',feutilb('getloss',1,model)/2);
cf=feplot(model); fecom('colordatagroup'); set(gca,'cameraupvector',[0 1 0])
One can have access to the piezoelectric material properties and the list of nodes associated to each pair of electrodes. Here nodes 1682 to 1685 are associated to the four pairs of electrodes defined in the model. The corresponding degree of freedom is the difference of potential between the electrodes in each pair corresponding to a specific piezoelectric layer. In this models, layers 1 and 8 are piezoelectric in groups 1 and 2 (the 6 internal layers correspond to the 6 layers of the supporting composite plate). Therefore only .21 (electrical) DOF is associated to nodes 1682-1685.
p_piezo('TabDD',model) % List piezo constitutive laws p_piezo('TabInfo',model) % List piezo related properties

Figure 2.2: Mesh of the composite plate. The different colours represent the different groups
The next step consists in the definition of the actuators and sensors in the model. Here, we consider one actuator on Node 1682 (layer 1 of group 1), the four piezoelectric patches are used as charge sensors, and the tip displacement of the cantilever beam is measured at node 1054. Note that in
order for Q-S1, Q-S2 and Q-S3 to measure resultant charge, the corresponding electrical difference of potential needs to be set to zero. If this
is not done, then the charge sensors will measure a charge close to zero (round-off errors) as there is no charge when the difference of potential
across the electrodes is free. For Q-Act, the electrical dof is already fixed due to the fact that the patch is used as a voltage actuator.
( d_piezo('TutoPlate_4pzt_single-s2')
)
d_piezo('TutoPlate_4pzt_single-s2')
)
%% Step 2 - Define actuators and sensors model=fe_case(model,'SensDof','Tip',1054.03); % Displ sensor model=fe_case(model,'DofSet','V-Act',struct('def',1,'DOF',1682.21)); %Act model=p_piezo('ElectrodeSensQ 1682 Q-Act',model); % Charge sensors model=p_piezo('ElectrodeSensQ 1683 Q-S1',model); model=p_piezo('ElectrodeSensQ 1684 Q-S2',model); model=p_piezo('ElectrodeSensQ 1685 Q-S3',model); % Fix dofs 1683-1685 to measure resultant (charge) model=fe_case(model,'FixDof','SC*1683-1685',[1683:1685]+.21); sens=fe_case(model,'sens');
In order to check the effect of the actuator, we compute the static response using the full model and represent the deformed shape (Figure 2.3).
( d_piezo('TutoPlate_4pzt_single-s3')
)
d_piezo('TutoPlate_4pzt_single-s3')
)
%% Step 3 Compute static and dynamic response d0=fe_simul('dfrf',stack_set(model,'info','Freq',0)); % direct refer frf at 0Hz cf.def=d0; fecom(';view3;scd .1;colordatagroup;undefline')
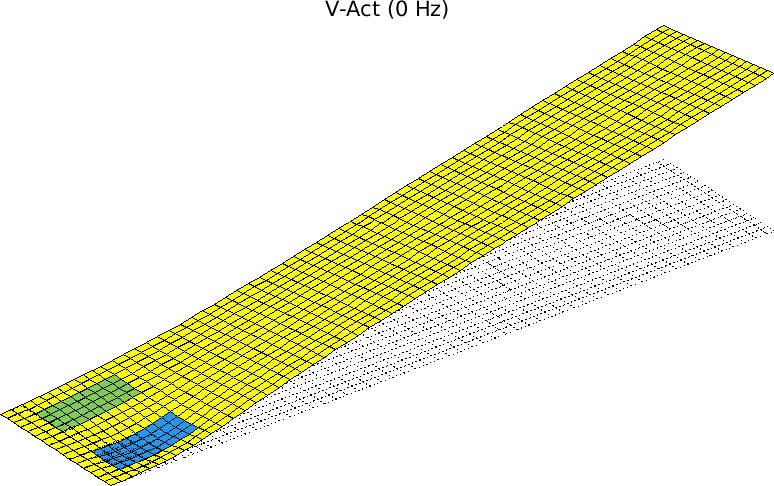
Figure 2.3: Deformed shape under voltage actuation on one of the bottom piezoelectric patches
We can now compute the transfer function between the actuator and the four charge sensors, as well as the tip sensor using the full model. The result is stored in the variable C1.
% Compute frequency response function (full model) if sdtkey('cvsnum','mklserv_client')>=126;ofact('mklserv_utils -silent') f=linspace(1,100,400); % in Hz else; f=linspace(1,100,100); % in Hz (just 100 points to make it fast) end d1=fe_simul('dfrf',stack_set(model,'info','Freq',f(:))); % direct refer frf % Project response on sensors C1=fe_case('SensObserve',sens,d1);C1.name='DFRF';C1.Ylab='V-Act'; C1.Xlab{1}={'Frequency','Hz'};
A reduced state-space model can be built and the frequency response function calculated, and stored in the variable C2. The two curves obtained are compared to show the accuracy of the reduced state-space model in Figure 2.4.
( d_piezo('TutoPlate_4pzt_single-s4')
)
d_piezo('TutoPlate_4pzt_single-s4')
)
%% Step 4 - Build state-space model [s1,TR1]=fe2ss('free 5 10 0',model); % C2=qbode(s1,f(:)*2*pi,'struct');C2.name='SS'; % Compare the two curves C2.X{2}=sens.lab; C1.X{3}=nor2ss('lab_in',s1);C2.X{3}=nor2ss('lab_in',s1);% C2=feutil('rmfield',C2,'lab'); C1.Ylab=C2.Ylab; ci=iiplot; iicom(ci,'curveinit',{'curve',C1.name,C1;'curve',C2.name,C2}); iicom('submagpha');
Error, width provided to ingraph must be from 5 to 95 from step of 5 Error, width provided to ingraph must be from 5 to 95 from step of 5
Figure 2.4: Comparison of FRF due to voltage actuation with the bottom piezo: full (DFRF) and reduced (SS) state-space models. Tip displacement and charge corresponding to electrical node 1682
Combination of electrodes can be used in order to build a variety of actuators and sensors. For example, using the four piezoelectric patches, it is possible to induce a pure bending in the cantilever plate by using the following combination: the two actuators on one side of the plate are combined (the same voltage is applied to both simultaneously), while the two actuators on the opposite side are combined and driven out of phase. This allows to cancel the in-plane effect of the patches and to induce a pure bending. If all 4 actuators are driven in phase, then it only induces in-plane forces causing displacements only in the plane of the plate (Figure 2.5).
The corresponding script to combine all four patches for bending and traction is:
( d_piezo('TutoPlate_4pzt_comb-s1')
)
d_piezo('TutoPlate_4pzt_comb-s1')
)
% See full example as MATLAB code in d_piezo('ScriptPz_plate_4pzt_comb') %% Step 1 - Build model and define actuator combinations model=d_piezo('MeshULBplate -cantilever'); % creates the model % combine electrodes to generate pure bending / pure traction data.def=[1 -1 1 -1;1 1 1 1]'; % Define combinations for actuators data.lab={'V-bend';'V-Tract'}; data.DOF=p_piezo('electrodeDOF.*',model); model=fe_case(model,'DofSet','V_{In}',data);
( d_piezo('TutoPlate_4pzt_comb-s2')
)
d_piezo('TutoPlate_4pzt_comb-s2')
)
%% Step 2 Compute static response d0=fe_simul('dfrf',stack_set(model,'info','Freq',0)); % direct refer frf cf=feplot(model); cf.def=d0; fecom(';view3;scd .02;colordataEvalZ;undefline')
The resulting static deflections of the plate are shown in Figure 2.6.
.png)
.png)
Figure 2.6: Static responses using a combination of actuators in order to induce pure bending or pure in-plane motion
We can now define two displacements sensors at the tip in the z and x directions and compute the FRFs between the bending actuator and the two displacements as well as the traction actuator and the two displacement sensors (Figure 2.7). The bending actuator/'Tip-z' FRF show three resonances corresponding to the first three bending mode shapes, while the traction actuator/'Tip-x' FRF shows no resonance due to the fact that the traction mode shape has a frequency much higher than the frequency band of the calculations. The FRFs show clearly the possibility to excite either bending or traction independently on the plate. The two other FRFs are close to zero.
( d_piezo('TutoPlate_4pzt_comb-s3')
)
d_piezo('TutoPlate_4pzt_comb-s3')
)
%% Step 3 - Dynamic response and state-space model % Add tip displacement sensor in x and z model=fe_case(model,'SensDof','Tip-z',1054.03); % Z-disp model=fe_case(model,'SensDof','Tip-x',1054.01); % X-disp % Make SS model and display FRF [sys,TR]=fe2ss('free 5 30 0 -dterm',model); C1=qbode(sys,linspace(1,100,400)'*2*pi,'struct'); C1.name='Bend-tract combination'; % Force name C1.X{2}={'Tip-z';'Tip-x'}; % Force input labels C1.X{3}={'V-bend';'V-tract'}; % Force output labels iicom('CurveReset');iicom('curveinit',C1)
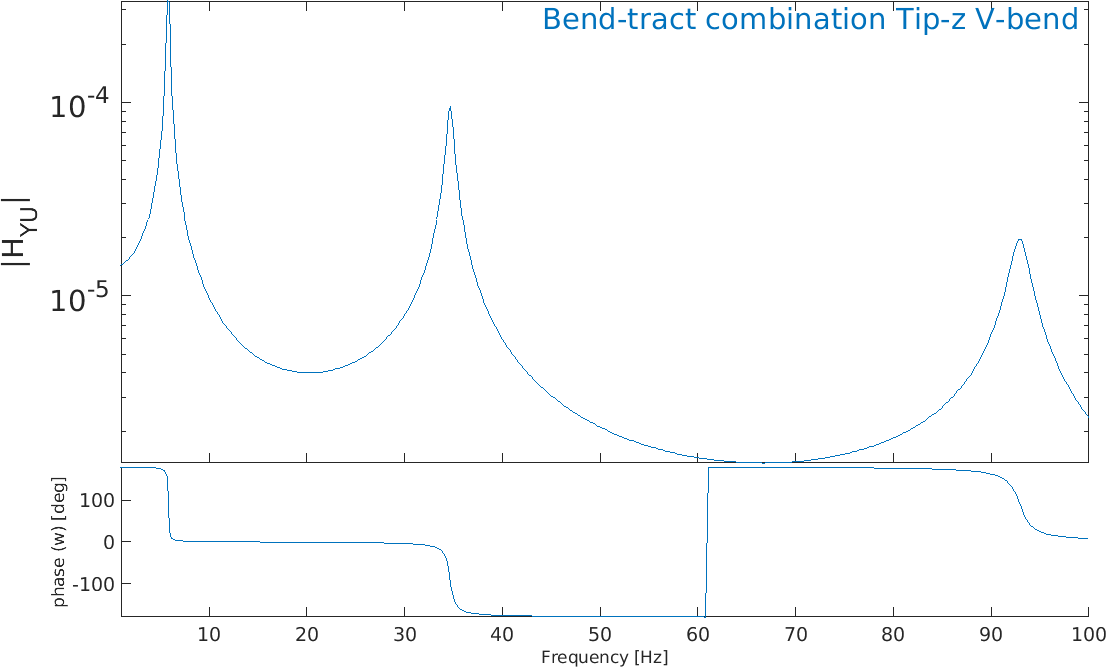

Figure 2.7: Bending actuator/'Tip-z' FRF (left) and traction actuator/'Tip-x' FRF (right)
Voltage and charge sensors can also be combined. Let us consider a voltage combination of nodes 1682 and 1683 for actuation, which will result in bending and a slight torsion of the plate due to the unsymmetrical bending actuation.
( d_piezo('TutoPlate_pzcomb_2-s1')
)
d_piezo('TutoPlate_pzcomb_2-s1')
)
% See full example as MATLAB code in d_piezo('ScriptPz_plate_pzcomb_2') %% Step 1 - Build model and define actuator combinations model=d_piezo('MeshULBplate cantilever'); % creates the model model=fe_case(model,'DofSet','V*1683-1682', ... struct('def',[1;-1],'DOF',[1682;1683]+.21));
( d_piezo('TutoPlate_pzcomb_2-s2')
)
d_piezo('TutoPlate_pzcomb_2-s2')
)
%% Step 2 - Compute static response d0=fe_simul('dfrf',stack_set(model,'info','Freq',0)); % direct refer frf cf=feplot(model); cf.def=d0; fecom(';view3;scd .1;colordatagroup;undefline')
We now define two sensors, consisting in charge combination with opposite signs for nodes 1684 and 1685
and voltage combination with opposite signs for the same nodes (Figure 2.8 shows the case of charge combination).
( d_piezo('TutoPlate_pzcomb_2-s3')
)
d_piezo('TutoPlate_pzcomb_2-s3')
)
%% Step 3 - Define sensor combinations % Combined charge output (SC electrodes) % difference of charge 1684-1685 r1=struct('cta',[1 -1],'DOF',[1684;1685]+.21,'name','QS3+4'); model=p_piezo('ElectrodeSensQ',model,r1); % Combined voltage output (OC electrodes) % difference of voltage 1684-1685 r1=struct('cta',[1 -1],'DOF',[1684;1685]+.21,'name','VS3+4'); model=fe_case(model,'SensDof',r1.name,r1);
By default, the electrodes are in 'open-circuit' condition for sensors, except if the sensor is also used as voltage
actuator which corresponds to a 'short-circuit' condition. Therefore, as the voltage is left 'free' on nodes 1684 and 1685,
the charge is zero and the combination will also be zero. If we wish to use the patches as charge sensors, we need to
short-circuit the electrodes, which will result in a zero voltage and in a measurable charge. This is illustrated by
computing the response in both configurations (open-circuit by default, and short-circuiting the electrodes for nodes 1684 and
1685):
( d_piezo('TutoPlate_pzcomb_2-s4')
)
d_piezo('TutoPlate_pzcomb_2-s4')
)
%% Step 4 - Compute dynamic response with state-space model [sys,TR]=fe2ss('free 5 10 0 -dterm',model); C1=qbode(sys,linspace(1,100,400)'*2*pi,'struct'); C1.name='OC'; % Now you need to SC 1684 and 1685 to measure charge resultant model=fe_case(model,'FixDof','SC*1684-1685',[1684;1685]+.21); [sys2,TR2]=fe2ss('free 5 10 0 -dterm',model); C2=qbode(sys2,linspace(1,100,400)'*2*pi,'struct');C2.name='SC'; % invert channels and scale C1.Y=fliplr(C1.Y); C1.X{2}= flipud(C1.X{2}); C2.Y(:,1)=C2.Y(:,1)*C1.Y(1,1)/C2.Y(1,1); iicom('curvereset'),iicom('curveinit',{'curve',C1.name,C1;'curve',C2.name,C2 });
The FRF for the combination of charge sensors is not exactly zero but has a negligible value in the 'open-circuit' condition, while the voltage
combination is equal to zero in the 'short-circuit' condition. Charge sensing in the short-circuit condition and voltage sensing in the open-circuit condition are compared by scaling the two FRFs to the static response (f=0 Hz) and the result is shown on Figure 2.9. The FRFs are very similar but the eigenfrequencies are slightly lower in the case of charge sensing. This is due to the well-known fact that open-circuit always
leads to a stiffening of the piezoelectric material. The effect on the natural frequency is however not very strong due to the small size of the piezoelectric patches with respect to the full plate.
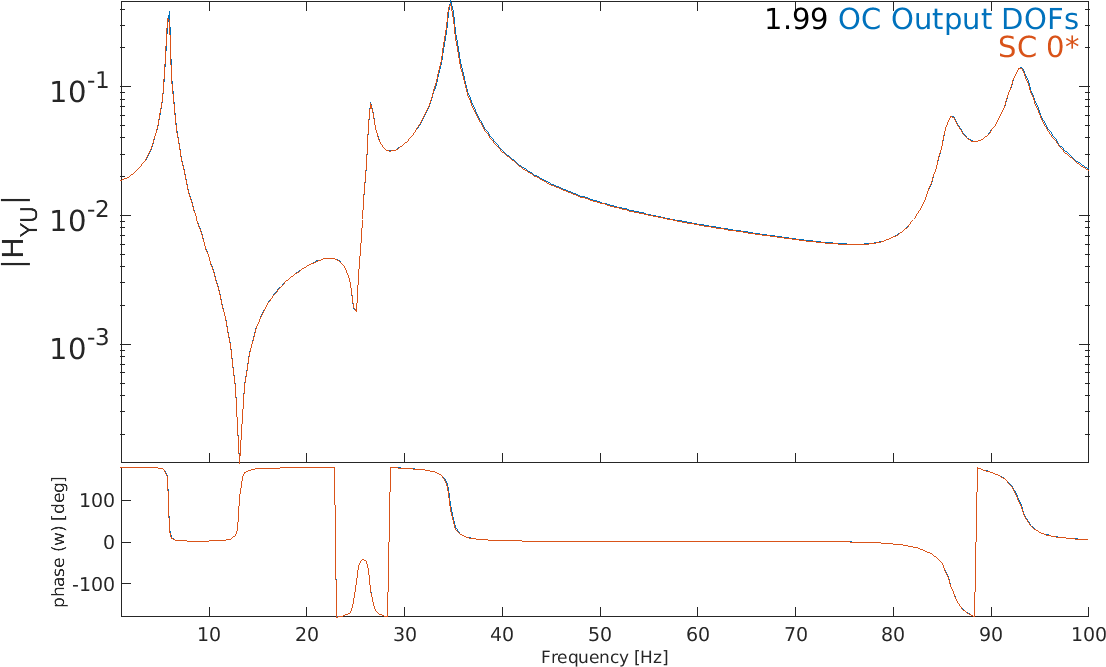
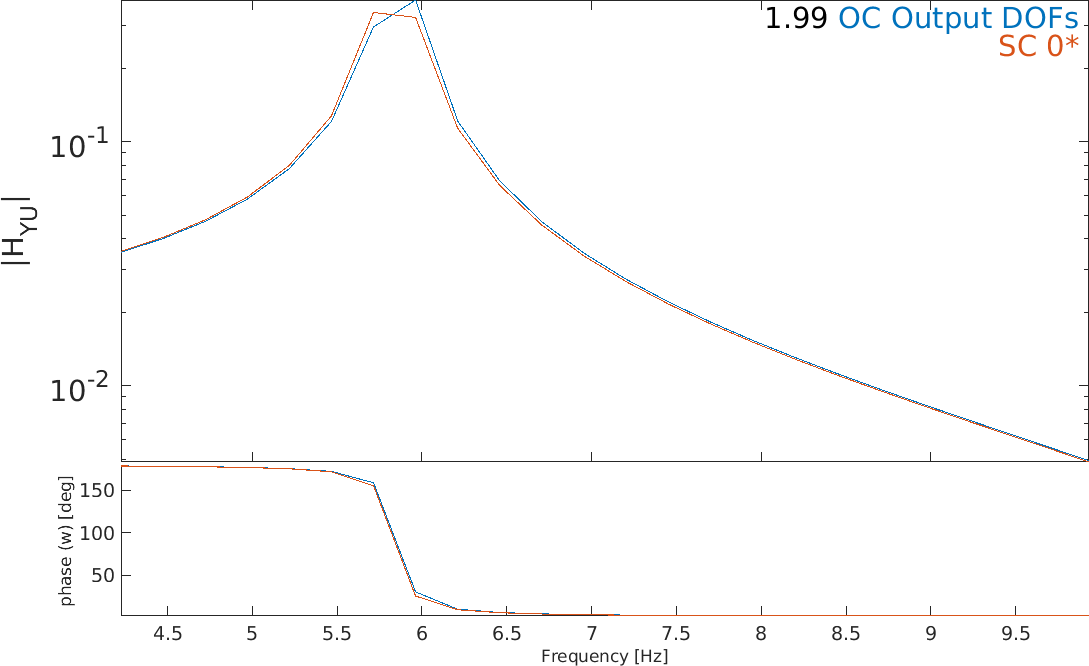
Figure 2.9: Comparison of FRFs (scaled to the static response) for voltage (green) and charge (blue) sensing. Zoom on the third eigenfrequency (right)
The stiffening effect due to the presence of an electric field in the piezoelectric material when the electrodes are in the open-circuit condition is a consequence of the piezoelectric coupling. One can look at the level of this piezoelectric coupling by comparing the modal frequencies with the electrodes in open and short-circuit conditions.
( d_piezo('TutoPlate_pzcomb_2-s5')
)
d_piezo('TutoPlate_pzcomb_2-s5')
)
%% Step 5 - Compute OC and SC frequencies model=d_piezo('MeshULBplate -cantilever'); % Open circuit : do nothing on electrodes d1=fe_eig(model,[5 20 1e3]); % Short circuit : fix all electric DOFs DOF=p_piezo('electrodeDOF.*',model); d2=fe_eig(fe_case(model,'FixDof','SC',DOF),[5 20 1e3]); r1=[d1.data(1:end)./d2.data(1:end)]; plot(r1,'*','linewidth',2);axis tight xlabel('Mode number');ylabel('f_{OC}/f_{SC}');
Figure 2.10 shows the ratio of the eigenfrequencies in the open-circuit vs short-circuited conditions. The difference depends on the mode number but is always lower than 1%. Higher stiffening effects occur when more of the strain energy is contained in the piezoelectric elements, and the coupling factor is higher.
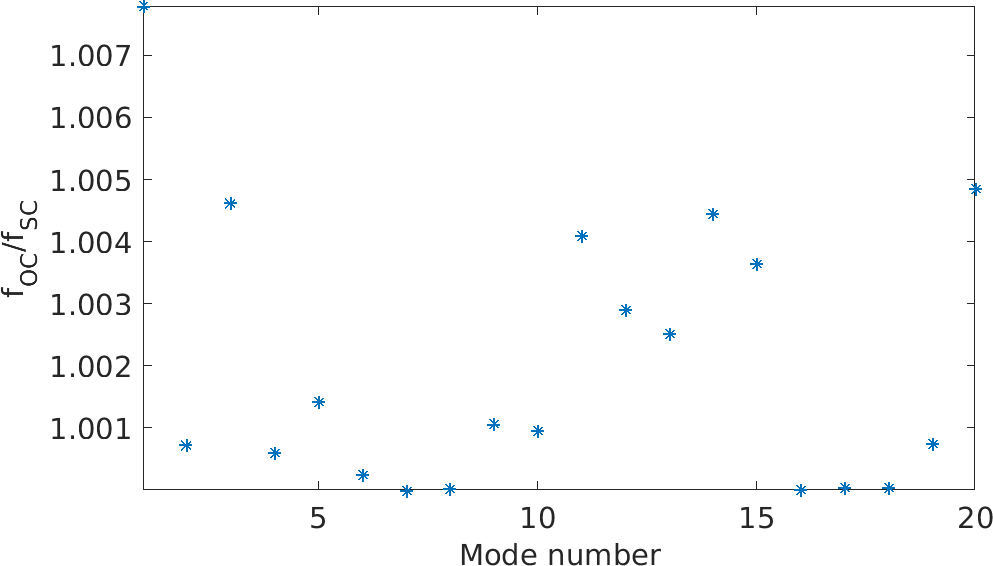
Figure 2.10: Ratio of the natural frequencies of modes 1 to 20 in open-circuit vs short-circuit conditions illustrating the stiffening of the piezoelectric material in the open-circuit condition


