In the series of our posts concerning model quality and connections, constraints regularization or penalization is a common topic. For contact-based coupling, these transformations introduce a gap/pressure relationship that often has a significant effect on the model behavior, statics and dynamics, that must be controlled.
➀ We will first discuss the concept of flexible contact coupling and how it is introduced in a model.
➁ Then we will illustrate the concept interest in application to some of our past projects:
👉 Railway brake friction block modal properties sensitivity to contact stiffness density under compression
👉 Bolted lap-joint modal properties evolution with contact preload and excitation amplitude for model lumping specification
👉 Considering uncontrolled contact surfaces on large welded stamped metal sheets dynamics of car body parts
👉 Wheel-to-ground stiffness tuning to reproduce brake squeal
Use cases illustrating the use of contact flexibility
I – Contact coupling and scale matters for Finite Elements Modelling
In statics, maximum interpenetration levels are controlled to be small regarding displacement and deformation to ensure a good enough solution. Considering physics and dynamics sensitivity, the coupling relationship must be coherent with the model and interface scale ratio but also account for model simplifications around the interface.
Ideally a contact constraint opposes the interpenetration between two bodies at their boundary, so that when the gap between both bodies closes a displacement constraint is applied, from which a coupling reaction force exists. In the same way in the case of friction, as long as there is no relative movement between the bodies, a coupling constraint exists at closed points from which a static friction reaction force exists.
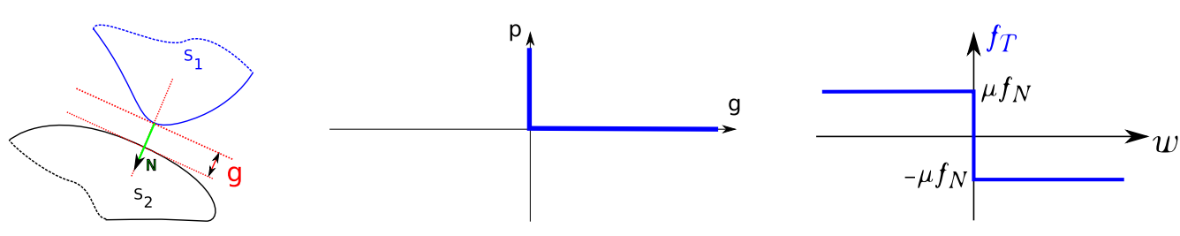
This idealization following the early concepts of Signorini (1930’s) and Coulomb (XVIIIth century) is rigorous for rigid bodies. In the real world however, nothing is infinitely rigid so that this notion must be associated to a scale. At the atomistic scale interpenetration exists between the electronic layers. At the roughness scale asperities come into contact, so that the surface mean plane at the body scale may see interpenetration.
Contact can thus be idealized in models using functional pressure/gap relationship at the scale of interest. Interpenetration is observed at the surface model scale (usually planar for finite elements models) and the relative pressure is observed on the contacting surface.
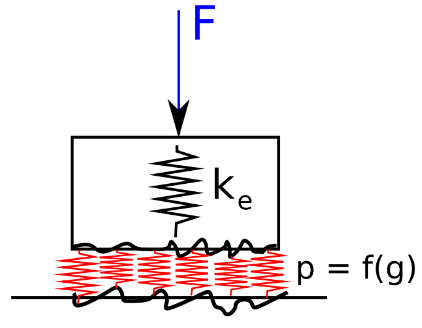
Functional contact model for FEM and sample contact laws in the form of gap/pressure relationship
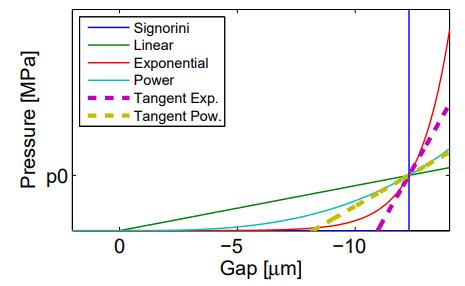
Many relationships can be devised, from a bilinear stiffness to any combination of power laws, including the exponential one. Power laws are seldom used in industrial applications, their choice is motivated by the notion of incompressibility observed in contact. They are more challenging to resolve in statics and can require several parameters that can discourage their use. Cubic laws are commonly used in the literature by analogy with the cubic spring response signature where third harmonics are also observed.
The pressure gap relationship graph also shows that depending on the law, the coupling stiffness at a given pressure varies. A calibration shall thus be performed as for the bilinear law to ensure a physical behavior. The functional representation will thus integrate all modeling simplifications – surface refinement, asperities, or even meta-modelling with 1D elements. It can then get flexible and store energy at the model scale. The next part of this post will illustrate in a few examples from our past projects what coupling sensitivity means in dynamics, and how this could be assessed in practice.
II – Contact coupling sensitivity for/from functional laws, a few illustrations
Connection flexibility can be exploited in many ways to alter response depending on the model and simulation context. The common aspect of the following examples is to estimate model dynamics sensitivity to connection flexibility as a basis for physical understanding, and engineering judgment regarding simulation needs. Model dynamics characterization is often based on parametric modal analysis, as used in the presented applications.
Railway brake friction block modal properties sensitivity to contact stiffness density under compression
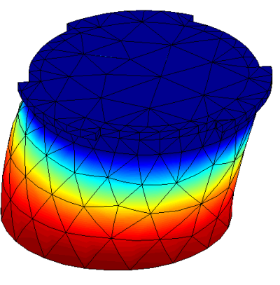
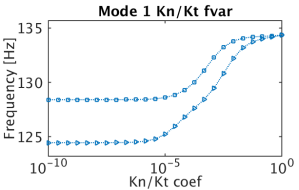
The first example illustrates the effect of contact stiffness density on a simple system’s dynamics. From [1] one of the friction lining blocks from a railway TGV braking pad is under study. Since it is a much softer material than the disc’s steel it will press, this study simplifies its characterization by considering a rigid plane for contact. The objective is to characterize the friction block bending modes that are visible in tests with a quasi-multiplicity associated to the number of blocks but potentially split due to their different loading.
The friction block It is clamped at its top through its fitting ring, and is in planar sliding condition (contact, no friction) on its base. Varying the contact stiffness density at the rigid base, the block frequencies evolve following an S-curve.
- If the stiffness is too low, the block behaves almost freely and generates an asymptote towards the free frequencies.
- Passed a stiffness threshold, that we call saturated, the interface faces a rigid connection equivalent to a clamped constraint, higher values do not change the behavior generating an asymptote towards the constrained frequency
- In between, there is a frequency transition where an interaction between the block and the connection exists. The connection stores energy, and it also influences damping.
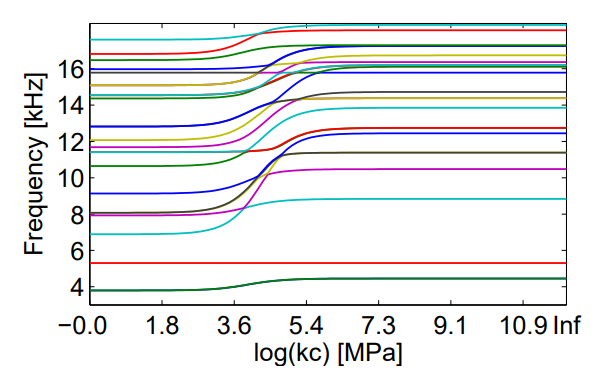
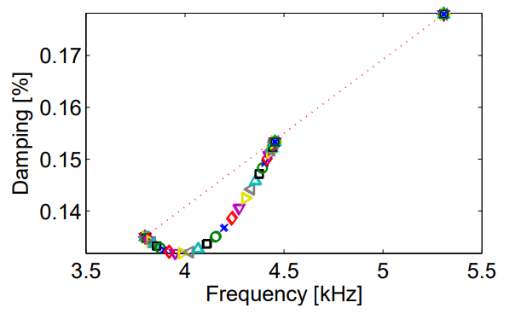
Friction block clamped sliding frequency and damping as function of contact coupling stiffness density (AcouFren project SNCF/ADEME)
Calibration can here be interesting to find a relevant coupling value that will produce the experimentally observed frequency, and that will cover asperity compression.
Bolted lap-joint modal properties evolution with contact preload and excitation amplitude for model lumping specification
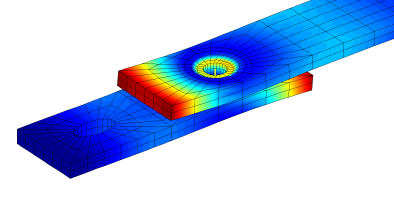
The second example from [2] illustrates how contact conditions can influence a system’s dynamics properties. In this example a cantilevered bolted lap joint first bending mode is studied as function of bolt preloading and vibration amplitude. These simulations were realized using an explicit scheme and a constant bilinear contact law. Dynamic characteristics were extracted from transient responses. A non-linear behavior is observed, as the frequency increases with prestress and evolves with amplitude. This is commonly observed in experiments.

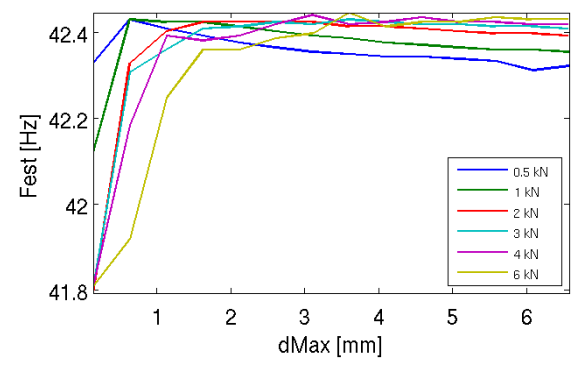
Bolted lap joint model. First bending mode frequency as function of pre-stress and vibration amplitude obtained by feature extraction of explicit non-linear transient simulations. (MAIAS project, EADS/PoleAstech)
The bolt preload drives the static contact surface around the bolt, then vibration amplitude alters this surface due to the bending shape. The effective coupling area thus varies, and the apparent coupling flexibility would feature a stiffness dependent on preload and amplitude.
A simplification using a 1D coupling element (meta-model) connecting the whole surface can then be used with an equivalent flexible connection whose stiffness will be parameterized.
Considering uncontrolled contact surfaces on large welded stamped metal sheets dynamics of car body parts
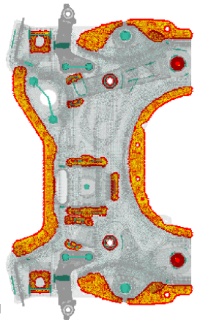
The third example from [3] illustrates how a flexible connection can cover uncertainty in a model and provide an averaged behavior. The engine cradle under study is an assembly of stamped steel sheet jointed with weld spots. A significant portion of the plates are thus touching each other without being constrained into contact. It is highlighted in yellow and red in the picture.

Contact potential location between two spot welded plates of an automotive engine cradle. First cradle mode frequency sensitivity as function of normal and tangential coupling stiffness outside weld spots (Collaboration with Stellantis).
The effective contact surface of a physical component is unknown and will certainly vary depending on production tolerances and process variation. A normal and tangential contact coupling sensitivity study on potential contact areas will characterize this feature criticality. With significant variations, the effect must be accounted for, either with a design allowing contacting surface control or by integrating the variability into the model for a robust design.
Wheel-to-ground stiffness tuning to reproduce brake squeal
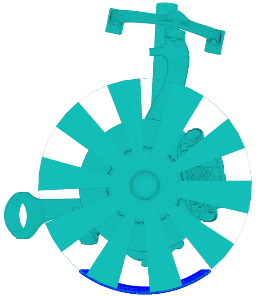
This last example [4] is extracted from a squeal simulation study. The low frequency noise appearing only on the vehicle in circulation implied including the wheel in the model. The rim model was added, and masses were fitted to add the tire mass. As correlation was challenged, we could locate incoherence on the rim, so that the question of its support arose. Typical free or clamped conditions were not satisfying.

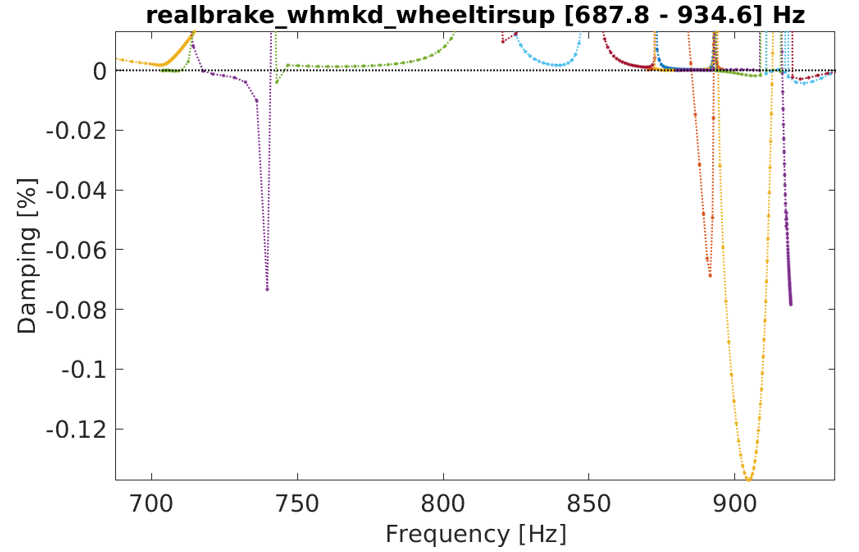
Squeal sensitivity to ground support integrating tire stiffness on the wheel. The rim is simplified for display only. (Collaboration with Mercedes-Benz).
The introduction of a flexible support highlighted that an unstable mode could be obtained in the model for a given range of stiffness coupling, and an optimum could be found from correlation. The optimal coupling value is coherent with a tire stiffness. It here could be identified without having to resort to complex estimations from tire specifications. Dynamic features are indeed not easy to extract from the usually provided Pacejka coefficients.
III – Conclusion
Contact modelling in mechanical assemblies must be coherent with the chosen scale and simplification levels. A flexible connection is then often physically relevant and can even be experimentally identified. Efficient implementation solutions must then be used to scan several orders of coupling stiffness magnitude, as in our communication [5] where saturated stiffness estimation and reduced order models are used to update the dynamic properties of contact interface. We’ll get back in more detail with these implementation aspects in a later post.
Thanks to our partners






References
[1] Benchmarking Signorini and exponential contact laws for an industrial train brake squeal application.
G. Vermot des Roches, O. Chiello, E. Balmes, X. Lorang.
ISMA, Leuven, 2012.
[2] Understanding friction induced damping in bolted assemblies through explicit transient simulation.
G. Vermot des Roches, E. Balmes
ISMA 2014.
[3] Error localization and updating of junction properties for an engine cradle model.
G. Vermot des Roches, E. Balmes, S. Nacivet
ISMA 2016.
[4] Model quality quantification and improvement based on operational squeal deflection shapes expansion
Guillaume Vermot des Roches, Martin Zacharczuk, Etienne Balmes.
EuroBrake 2023. EB2023-MSL-005.
[5] Updating and design sensitivity processes applied to drum brake squeal analysis.
G. Martin, E. Balmes, G. Vermot des Roches, T. Chancelier
Eurobrake 2016.
