In partnership with the “SOURCE” ANR project, SDT has been used by the DISCoH researcher’s team from PIMM laboratory (Nassim Benbara, Marc Rebillat and Nazih Mechbal) to identify a polypropylene plate material property temperature dependency. A summary of this work is provided below and more detailed explanations (among other results) have been published in [1].
The plate is fitted with two piezoelectric patches, one used as an actuator, the other as a sensor. A sweep signal (100 – 1500 Hz) is sent to the actuator and the transfer function between this signal and the voltage measured by the sensor is built.
To assess the influence of temperature, the plate is placed in an oven equipped with a temperature sensor. It is drilled at two corners and suspended in the oven using two nylon wires, which effectively decouple the vibratory behavior of the plate itself from its environment (grid, vibration of the oven’s internal walls, etc.).

The measurement protocol is defined as follows:
- A temperature hold is applied to homogenize the plate temperature.
- A temperature ramp from 0 to 60°C is defined, slow enough to avoid significant temperature gradient across the plate (approx. 1°C/min).
- An automatic measurement is triggered every two minutes to obtain a series of transfers at different temperatures.
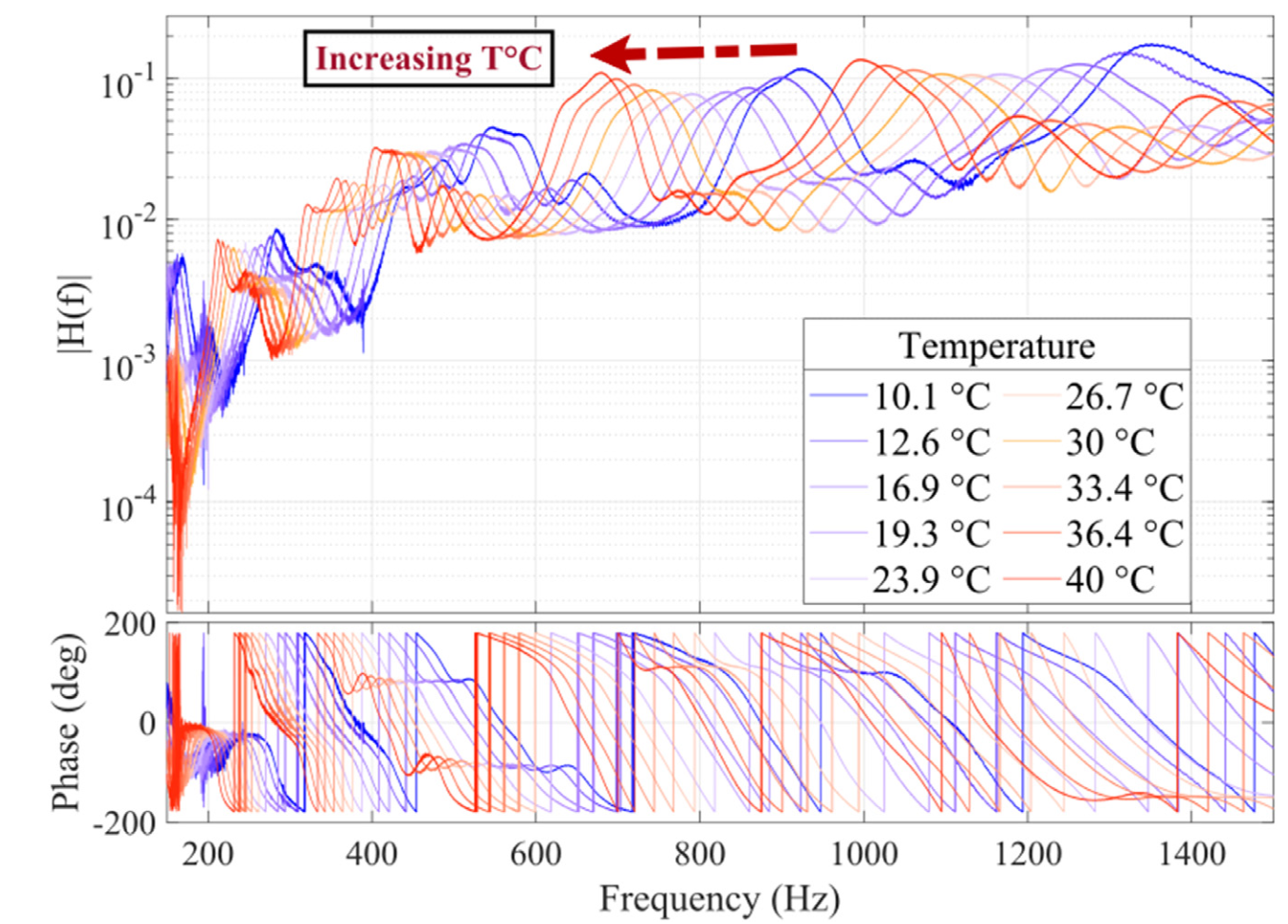
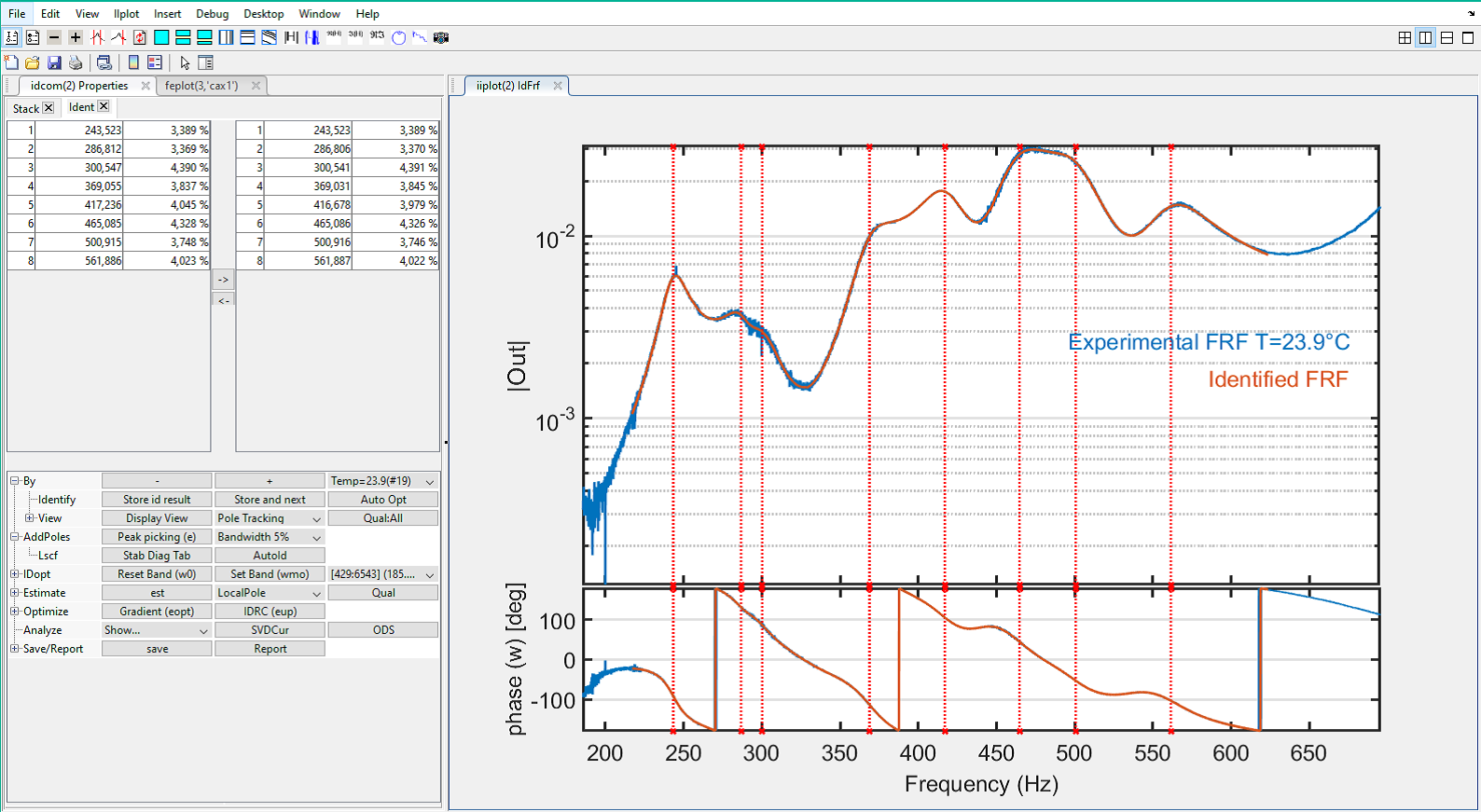
To assess temperature influence, the strategy is to identify the system’s modes (frequency and damping) and analyze their evolution with temperature. A dedicated strategy has been implemented in the SDT toolbox to avoid manually identifying all the transfers, and to enable automated post-processing of the results:
- Initialize modes on transfers corresponding to the first temperature
- Automatic, sequential optimization of poles from one temperature to another
- Construction of a database containing the evolution of all frequencies and modal damping associated with each measurement temperature.
- Generate curves to analyze results.
Analysis of the evolution curves shows that the modes are highly sensitive to temperature, with maximum damping of around 4% around 20°C. Modal frequencies evolve by +/- 25% compared to the reference temperature of 25.4°C.
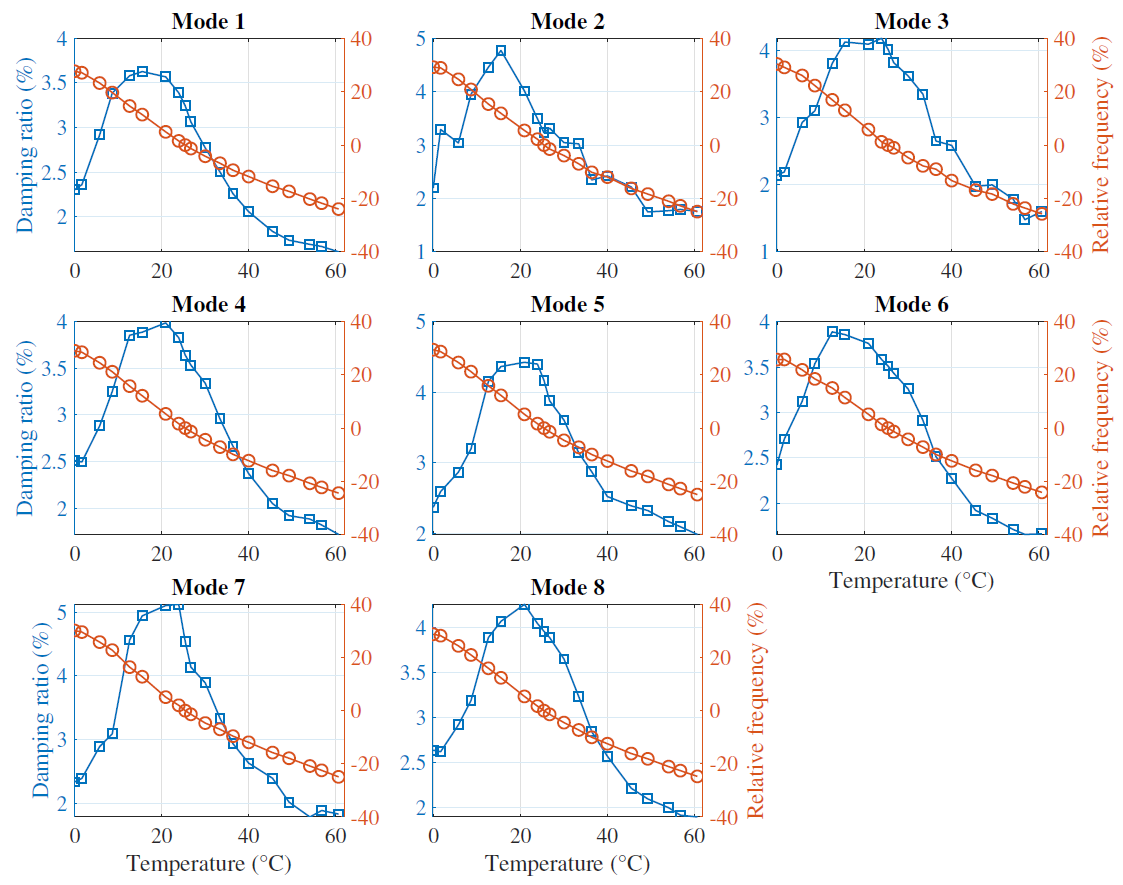
The evolution with temperature of each mode is very similar, which was expected given that the material can be considered isotropic: the evolution of the Young’s modulus E(T) impacts all modes equally. The small differences can be explained by
- a possible degree of anisotropy
- a temperature gradient in the plate
- identification bias
In addition to analyzing the influence of temperature on modes, the second objective was to identify the relation between the Young’s modulus and temperature. To achieve this, the system has been modelled in SDT, including the piezoelectric patches whose geometry and properties are available in SDT libraries.

Classical model updating would have tried to minimize the difference between the model and test mode frequencies. The PIMM’s researchers preferred to work on the comparison of transfers directly. The advantage of this strategy is that modal identification is no longer necessary, provided that the test is of good quality, and that the modes haven been first identified. The simulated transfer is obtained in SDT by entering the actuator voltage as input and the receiver voltage as output. The aim is then to use an optimization loop to find the material parameters that minimize the difference between synthesized and measured transfers, for all temperatures.
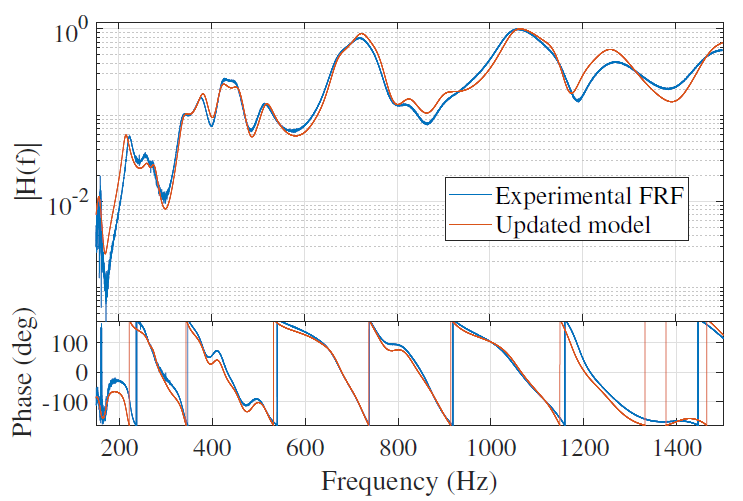
To limit the number of unknown parameters in this work, the loss factor was fixed to twice the average identified damping at each temperature. First updating attempts showed that it was difficult to obtain a good superposition by only varying the Young’s modulus. Poisson’s ratio was thus considered as an additional parameter. This greatly improved trtansfers superposition and led to the identification of the following material dependency to temperature:

The study’s strategy implemented in SDT to identify model parameters is finally summarized in the figure below.
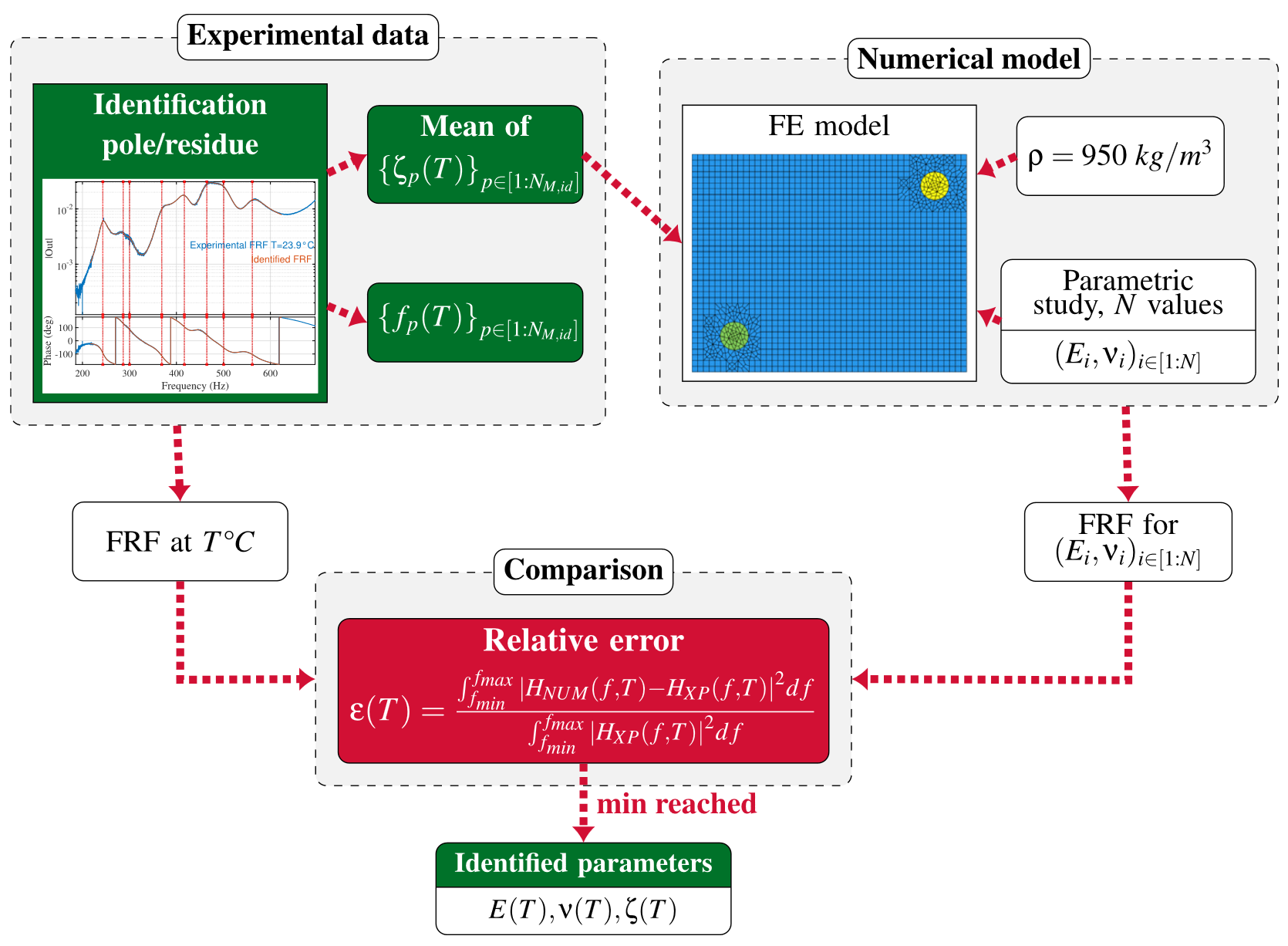
To be completely independent from modal identification (and perhaps to further improve the quality of recalibration), material loss factor should also be a model parameter, in the same way as Young’s modulus and Poisson’s ratio. This was kept as an improvement perspective of this work.
It is worth mentioning that the influence of Poisson’s ratio on model updating has been little studied and that the variation, at least for this specific test case, is not negligible.
References
[1] Bending waves focusing in arbitrary shaped plate-like structures: Study of temperature effects, development of a digital twin and of an associated neural-network based compensation procedure.
N. Bernbara, G. Martin, M. Rébillat, N. Mechbal. Journal of Sound and Vibration,Volume 526, 2022.
