Guilherme Malacrida Alves will defend his PhD thesis on “Experimental modal analysis of time varying non-linear systems. Application to brake squeal”
Subject to defense authorization, it will take place
🕓 on Wednesday, January the 29th at 2 p.m
📌 at Amphi A – 151 Boulevard de l’hopital 75013 Paris (Arts & Métiers Paristech Paris campus)
The jury will be composed of
Franck MASSA, Professeur, Université Polytechnique Hauts-de-France, LAMIH – Rapporteur
Gaël CHEVALLIER, Professeur, Ecole de l’Air et de l’Espace – Rapporteur
Jean-Luc DION, Professeur, ISAE-Supmeca, Quartz – Examinateur
Etienne BALMES, Professeur, Arts et métiers science et technologies, PIMM – Examinateur
Guillaume MARTIN, Docteur, SDTools – Examinateur
This thesis has been directed by Etienne Balmes with industrial support by Guillaume Martin for SDTools and the contribution of Hitachi Astemo.
🔑 Keywords
Brake squeal instability, Nonlinear vibrations, Limit cycle, Parameter-varying systems, Signal model, Experimental modal analysis, 3D-SLDV, Instant stiffness, clustering.
📝 Abstract
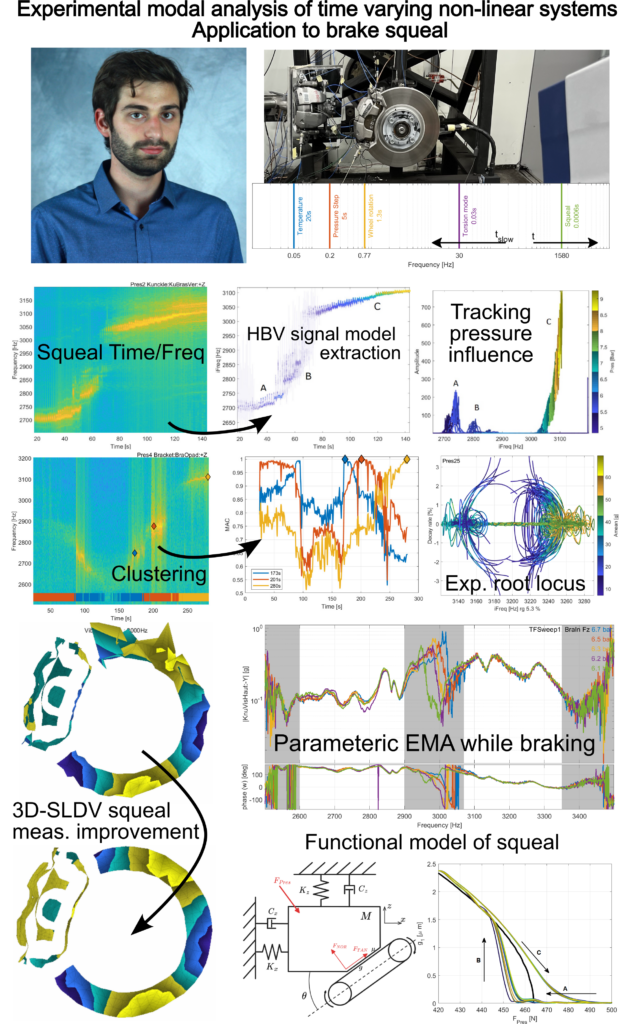
Brake squeal is a complex phenomenon resulting from a mode coupling instability. Despite being a subject of study for many years, no robust design method exists for its prevention and correcting measures are heavily based on prototyping and validation, which is time-consuming and expensive. Squeal testing can be separated into three main activities: classification of squeal occurrences based on acoustic levels, detailed spatial characterization of limit cycles, and modal characterization of components and assemblies. This work thus seeks to propose and analyze the usefulness of different methodological changes to testing methods. A specificity of squeal is that vibration depends on multiple operating parameters pressure, wheel speed, temperature, … which vary in time relatively slowly compared to the frequencies of squeal limit cycles. It is thus necessary to take this specificity into consideration to design testing methods and analyze their results. As a mean to gain further insight on the effects of slowly changing operating conditions, a new functional model for squeal is proposed based on the well-known Hoffmann model. The novelty lies in replacing the variable friction assumption by a nonlinear contact law, which introduces a sensitivity to the applied pressure (as the static-state is modified), and amplitude (through its effect on the mean pressure). Analyzing and comparing the response of this model in frequency and time domain provides a path to understanding the relations between squeal limit cycle vibration and parameters. The definition of a Harmonic Balance Vector (HBV) signal model and the use of demodulation for its estimation, then allows tracking of quasi-periodic squeal signals without resolution limitations of the Fourier transform. For parametric squeal tests, this method improved occurrence classification by extracting the evolutions of features such as instantaneous frequency, global vibration amplitude, generalized coordinates and shape. For the detailed shape analysis using 3D-SLDV measurements, the HBV signal estimates led to results improved over current methods based on short time Fourier transforms. Applications are illustrated in a contact test bench to obtain the evolution of shapes with pressure, and in a full-scale brake test to obtain the limit cycle shapes. The HBV signal estimation can also extract spatially detailed shapes for higher harmonics. Two indicators (harmonic modulation and harmonic perturbation) are then proposed, based on the notion of instant stiffness, as a mean of evaluating where in a period the system is stiffer or softer. Finally, for in operation parametric Experimental Modal Analysis (EMA), full scale tests showed that modes away from squeal can be consistently identified and tracked. Near squeal, however, the presence of a coherence loss indicates that other methods are required such as the feedforward phase resonance tracking proposed in the analysis of the simplified contact test bench.
📜 Publications
Analysis of a brake squeal functional model using a linear parameter varying perspective
G. Malacrida Alves, E. Balmes, G. Martin
INTER-NOISE 2024
Parametric modal testing using slow but continuous variation of operating conditions. Illustration on a contact bench.
Malacrida Alves, E. Balmes, G. Martin, T. Chancelier, E. Kassa
SURVISHNO 2023
A time varying system perspective on rubber mount tests
G. Malacrida Alves, E. Balmes
ISMA 2022
You are all welcome!
